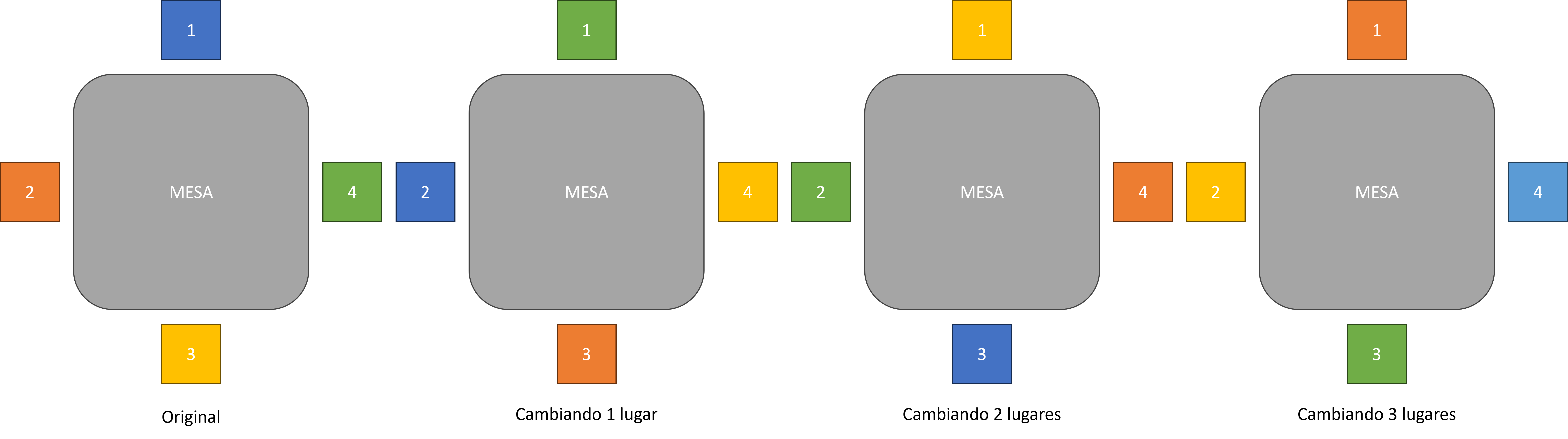
Imagina que Norma compró cinco libros para leer en vacaciones y quiere ordenarlos para leerlos, ¿de cuántas maneras puede hacerlo?

Si aplicamos el Principio General de la Multiplicación para elegir el primer libro Norma tiene 5 opciones, para el segundo 4, para el tercero 3, para el cuarto 2 y el último sólo 1 porque es el que sobra. Así que las formas de ordenar su lectura son 5⋅4⋅3⋅2⋅1=120

Habiendo observado lo anterior, podemos pensar, en un planteamiento más general, ¿de cuántas formas podrías ordenar los elementos de un conjunto de n elementos, siendo n un número natural?

Para elegir el primer objeto tenemos \(n\) opciones, para elegir el segundo \((n−1)\) opciones, para elegir el tercero \((n−2)\) opciones y así sucesivamente. Cuando queden dos objetos por ordenar tomaremos una de las dos opciones y finalmente el objeto que sobre ocupará el último lugar, así la cantidad de maneras de ordenar esos \(n\) objetos es:

\(n×(n−1)×(n−2)×⋯×3×2×1\)

De manera que la cantidad que buscamos es el producto de los primeros n números naturales. A multiplicar a n por todos los enteros positivos anteriores a él le llamamos factorial de n y se representa por el símbolo \(n!\). La solución del problema anterior puede expresarse simplemente por \(5!=120\) 

Llamaremos Permutaciones de n objetos a la cantidad de formas en las que pueden ordenarse, acomodarse, organizarse, enlistarse, etc., n objetos distintos de un conjunto, y  las denotaremos como:

\(Pemutaciones\:de\:n\:objetos\:distintos→P_{n}=n!\)

Las permutaciones o acomodos son formas de organizar por completo un conjunto de \(n\) elementos. Considera las permutaciones como las listas posibles que puedes hacer de un conjunto de elementos. Dicho de otra manera, cuando en un problema tengas que organizar TODOS los elementos de un conjunto que tiene todos sus elementos distintos bastará con calcular sus permutaciones.

Nota: El número 0!=1 porque representa las formas de organizar 0 objetos, que se logra de una sola forma. 

Teniendo en cuenta que 1!=1,2!=2,3!=6 intenta calcular los factoriales de los números del 4 al 10.

Ahora piensa que tú y tres amigos van a comer a un restaurante, ¿de cuántas formas podrían sentarse en una mesa con cuatro lugares?

Pensemos en que podemos numerar la mesa como en la siguiente imagen.

Podríamos pensar en que como hay que organizar a cada quien en un asiento el problema se reduce a \(P_{4}=4!=24\) formas. Sin embargo, es necesario considerar qué pasaría si le pedimos a los cuatro que se corran hacia su derecha un asiento, la mesa estaría acomodada de forma distinta? ¿Y si les pedimos que lo hagan una vez más? Bueno, esos acomodos podrían interpretarse más o menos así

Podemos ver que la silla azul siempre está entre la verde y la salmón, y lo mismo pasa con las demás sillas, todas conservan su posición relativa con las demás. No obstante, como permutaciones son distintas, esto significa que si contamos las permutaciones de 4 elementos estamos contando 4 veces cada una de esas permutaciones, entonces deberíamos dividir el resultado entre 4, entonces el número de formas de sentarse es de \(\frac{4!}{4}=3!=6\)

En general, dados n objetos diferentes, cada acomodo de estos al rededor de un círculo se le llama permutación circular. Entonces, las permutaciones circulares son las distintas formas de organizar por completo un conjunto de objetos de n elementos al rededor de un círculo, considerando que al girar los elementos de su posición al rededor del círculo se mantiene la misma posición relativa con el resto de los elementos. Se calculan como: 

\(P_{C,n}=\frac{n!}{n}=(n−1)!\)