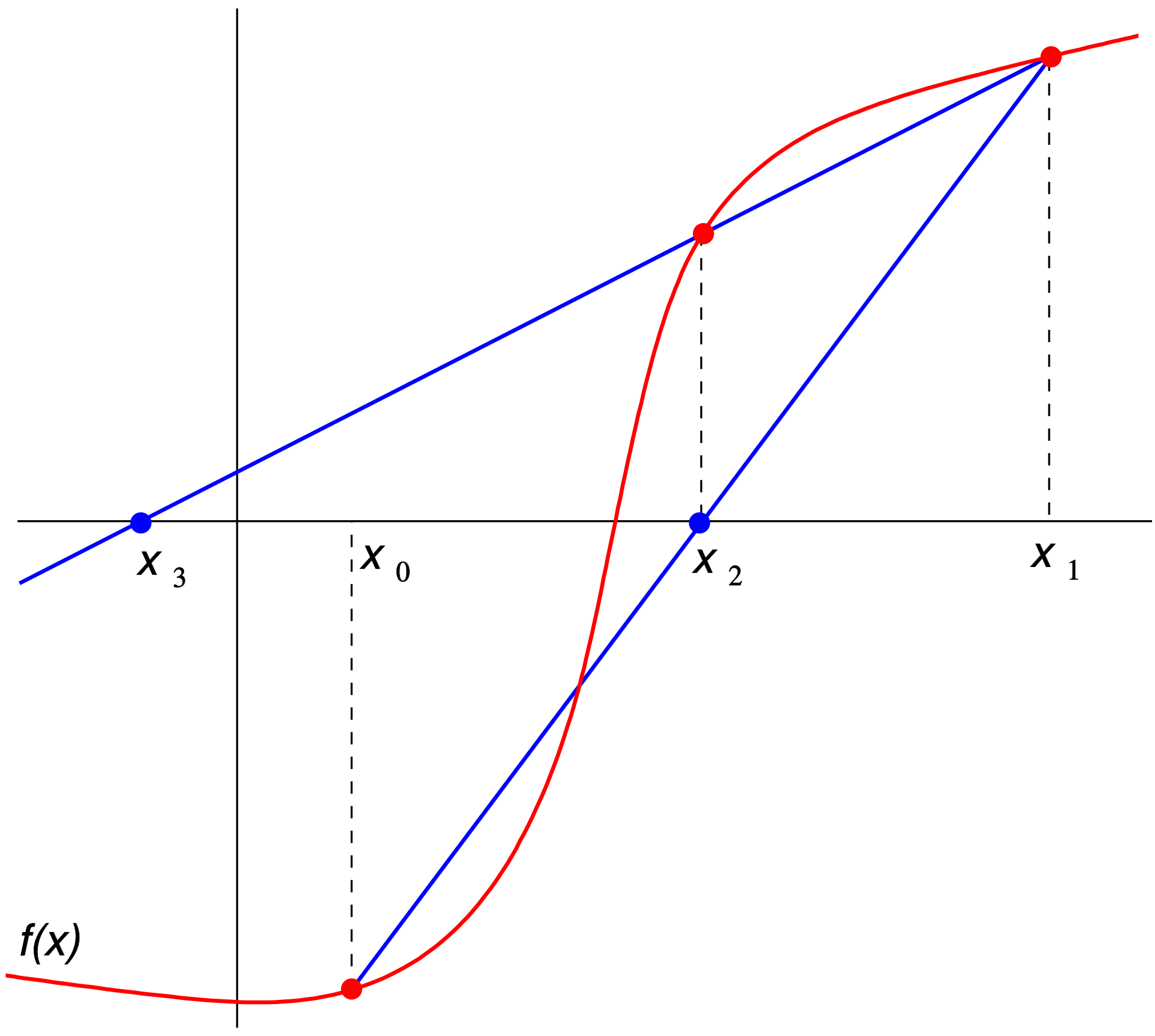
SECANTE: En matemáticas, el método de la secante es un algoritmo de búsqueda de cruces por cero que trabaja con dos puntos iniciales y una proyección al eje de las ordenadas, el cruce por este eje define el nuevo punto que sustituirá al punto mas antiguo.
Un problema obvio que surge con el método de la falsa posición es que dependiendo de la función, el intervalo de búsqueda puede que no decrezca. El problema se puede evitar si se consideran los puntos en sucesión estricta en el sentido de que el valor más viejo es descartado y sólo se usan los dos valores más recientes para el cálculo del nuevo valor. Esta idea conduce al método de la secante.
El método se basa en obtener la ecuación de la recta que pasa por los puntos (xn−1, f(xn−1)) y (xn, f(xn)). A dicha recta se le llama secante por cortar la gráfica de la función.
El método de la secante inicia con dos valores establecidos y a partir de esos valores genera un tercer valor haciendo una proyección de la recta secante hasta cruzar el eje de las ordenadas.
INSTRUCCIÓN: Antes de resolver el ejercicio vea el video donde se explica el método de la secante.
A partir de la ecuación f(x) = x-2cos(x), con x1=1 y x2=1.5; calcular el cruce por cero dentro de este intervalo.
% Método de la secante para calculo de cruces por cero de una función no lineal que se mueve en plano real.
clear all
a=1; % a -- Limite inferior del intervalo
b=1.5; % b -- Limite superior del intervalo
Err = 1; % Inicializa el error para ingresar al ciclo iterativo.
tol = 1e-6; % Tolerancia especificada para la convergencia.
fa = a - 2.*cos(a); % Valor de la función al inicio del intervalo
fb = b - 2.*cos(b); % Valor de la función al final del intervalo
Mat = [a fa; b fb]; % Inicializa la matriz para almacenar datos generados
c = 2; % Contador de iteraciones, inicia en dos pues se antemano se tienen dos calculos
while Err > tol & c < 20
h = a - fa*(b-a)/(fb-fa); % Punto de cruce de la recta secante con el eje x
fh = h - 2.*cos(h); % Valor de la funcion en el punto de cruce
c = c + 1; % Contador de iteraciones para no dejar ciclado el programa en caso de alguna inconsistencia
Mat(c,:) = [h fh]; % Matriz que almacena los resultados de cada iteracion
% Los nuevos puntos para la siguiente iteracion son
a = b; fa = fb;
b = h; fb = fh;
Err = abs(fh); % Criterio de error
end
Mat. % Cruce por cero que determina el metodo de la secante
Cero = h
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0