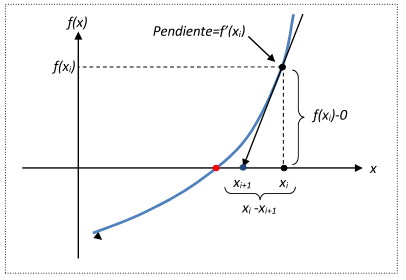
NEWTON-RAPHSON: El método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo para encontrar aproximaciones de los cruces por cero de una función real.

El método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo para encontrar aproximaciones de los cruces por cero de una función real.

INSTRUCCIÓN: Antes de resolver el ejercicio vea los videos donde se explica el método de Newton Raphson.

A partir de la ecuación f(x) = cos(x)-3x, con x0=0.5; calcular el cruce por cero al cual converge el método.

% Funcion del metodo de Newton-Raphson para calculo de cruces por cero
% de una funcion no lineal que se mueve en plano real.
clear all
clc
 
a=0.5; % a -- Punto de arranque del metodo
Err = 1; % Inicializa el error para ingresar al ciclo iterativo.
tol = 1e-12; % Tolerancia especificada para la convergencia.
c = 0; % Inicializa el contador de iteraciones
 
while Err > tol & c < 20
% Valor de la funcion en el punto de arranque
fa = cos(a) - 3*a;
% Valor de la derivada de la funcion en el punto de arranque
fpa = -sin(a) - 3;
% Calculo del nuevo valor de x dado por el metodo de Newton-Raphson
xn = a - fa/fpa;
% Valor de la funcion en el nuevo punto
fxn = cos(xn) - 3*xn;
% Contador de iteraciones para no dejar ciclado el programa en caso de alguna inconsistencia
c = c + 1;
% Matriz que almacena los resultados de cada iteracion
Mat(c,:) = [a fa fpa];
% Asignacion de la aproximacion mas nueva para seguir la iteracion
a = xn;
% Criterio de error
Err = abs(fxn);
end
 
% Cruce por cero que determina el metodo de Newton-Raphson
Mat
Cero = xn