La solución del problema se plantea en términos de que se requiere encontrar el valor de f tal que f(x)=0. Para iniciar el método, se determinan dos puntos x₀ y x₁ en los cuales la función toma valores con signo opuesto. Asumiendo que la función es continua, con el teorema del valor intermedio se garantiza que debe de existir un cruce por cero de f entre x₀ y x₁. La función se evalúa entonces en el punto x₂=½(x₀ + x₁). El punto x₃ se elige como el punto del par (x₀ , x₁) en el cual el valor de la función tenga signo opuesto a f(x₂). Se obtiene así un intervalo [x₂ , x₃] que continua conteniendo un cruce por cero y que tiene la mitad del tamaño del intervalo original. El proceso se repite hasta que los límites superior e inferior del cruce por cero están suficientemente cercanos. La figura 1 muestra un paso típico de este método. El método se detiene cuando Ιx_n-x_n-1Ι<tol ó  Ιf(x_n+1)Ι<tol donde tol es la tolerancia especificada para el método de bisección.

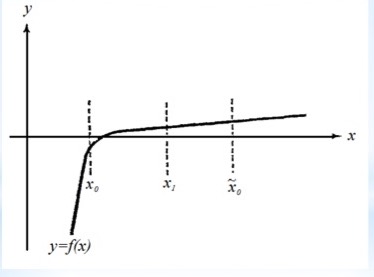
                                             FIGURA 1.- Método de bisección.

El método de bisección tiene la ventaja de ser simple, sin embargo, la velocidad de convergencia es lenta y cuando las iteraciones se aproximan al cruce por cero es mejor usar otro método con convergencia más rápida. La convergencia del método de bisección solo se asegura a partir de los siguientes resultados.

TEOREMA 2.1.- Suponiendo que f es continua en el intervalo [x₀ , x₁] y f(x₀)*f(x₁)<0, el método de bisección genera una sucesión {xn}^∞_n=0 que aproxima x* a un cruce por cero de f, tal que

           Ιx_n-x*Ι≤(x₀-x₁)/2n,      n≥1

Este último teorema implica que

             x_n=x*+O(1/2ⁿ)

donde O(1/2n) es la velocidad de convergencia del método. Se tiene además que el método de bisección satisface

           lim(x_n+1-x*)/(x_n-x*)=1/2.    cuando n→∞

por lo que el método converge linealmente.