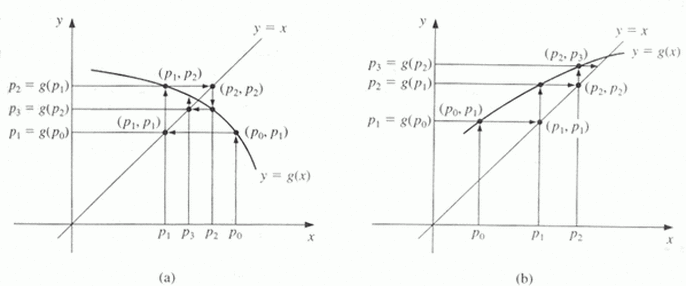
PUNTO FIJO
PUNTO FIJO: Este método buscar un cruce por cero de una función a partir de un valor inicial, una tolerancia y un numero "n" de iteraciones. Para tener en cuenta, en este método no es necesario el uso de intervalos sino de un punto inicial o de arranque.