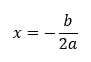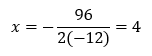a. ¿Cuánto tiempo tarda la pelota en alcanzar su altura máxima?
Respuesta: 4 segundos
El tiempo que tarda el balón en alcanzar su altura máxima se obtiene con la coordenada x del vértice, ya que es el punto máximo de la parábola. Éste se calcula:
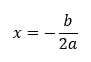
Por lo tanto,
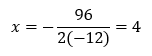
b. ¿Cuál es la altura máxima que alcanza cada pelota?
Respuesta: 292 metros
La altura máxima que alcanza el balón se da en la coordenada y del vértice de la función. Por lo tanto, evaluamos la función en 4.
f(4)=-12(4)²+96(4)+100=292
c. ¿Qué altura alcanza la pelota después de 3 segundos?
Respuesta: 280 metros
Evaluamos la función en 3.
f(3)=-12(3)²+96(3)+100=280
Completa la siguiente tabla del tiempo del balón que se indica:
Se evalúa la función en cada uno de los segundos dados:
f(0)=-12(0)²+96(0)+100=100
f(1)=-12(1)²+96(1)+100=184
f(2)=-12(2)²+96(2)+100=244
f(3)=-12(3)²+96(3)+100=280
f(4)=-12(4)²+96(4)+100=292
f(5)=-12(5)²+96(5)+100=280
f(6)=-12(6)²+96(6)+100=244
f(7)=-12(7)²+96(7)+100=184
f(8)=-12(8)²+96(8)+100=100
¿Cuánto dura la trayectoria del balón?
Respuesta: 8 segundos
En la tabla anterior nos damos cuenta que en el segundo 8 es vuelve a llegar a la altura inicial. Por lo tanto, son 8 segundos los que tarda en hacer su trayectoria.
en la parte inferior para ver tu puntuación.
en la parte inferior.
para ver el procedimiento para resolver el ejercicio.