Definición:
El peso de un árbol generador es la suma de los pesos de las ramas del árbol. Un árbol generador mínimo es uno con peso mínimo.

Una interpretación física de este problema es considerar los vértices de un grafo como ciudades, y los pesos de las aristas como los costos de construcción y mantenimiento de vías de comunicación entre las ciudades. Supongamos que queremos construir una red de comunicaciones que conecte a todas las ciudades a un costo mínimo. Entonces el problema es determinar un árbol generador mínimo.

Un procedimiento para resolver este problema se base en la observación de que entre todas las aristas en un circuito, la arista con mayor peso no esta en el árbol generador mínimo. Sea "C" un circuito en un grafo pesado, y "E" la arista con el mayor peso en "C". Supongamos que "E" es una rama de un árbol generador de T. Sea d el conjunto de corte correspondiente a la rama a la rama "E" como el circuito C y el conjunto de corte d deben tener un numero par de aristas en común además de la arista "E" deberán existir al menos una o más aristas que estén tanto en C como en D. Sea F una de estas aristas. Observemos que F es una cuerda del árbol generador t debido a que D es un conjunto de corte. Agreguemos la arista F al árbol generador T y denotemos el subgrafo resultante como U. Es obvio que U es un subgrafo generador que contiene exactamente un circuito, el circuito correspondiente a F. Si eliminamos E de U, obtenemos un árbol generador cuyo peso es menor que T.

Construiremos un subgrafo del grafo pesado paso por paso, al ir examinando cada arista en orden creciente de pesos. Se agregara una arista al subgrafo parcialmente construido si no origina un circuito, y será descartada en caso contrario. La constricción termina cuando todas las aristas han sido examinadas. Es claro que nuestra construcción de origen a un subgrafo que no contiene un circuito. El subgrafo también es conexo. Así el subgrafo construido es un árbol.

Además, este es un árbol generador debido a que el grafo originales es conexo. Finalmente, el árbol generador es mínimo por que en el proceso de construcción una arista era excluida a favor de las aristas de pesos mayores solo si sé sabia que la arista excluida no podía estar en un árbol generador mínimo. En otras palabras, las v - 1 aristas en el subgrafo son efectivamente las v - 1 aristas con los pesos menores que pueden ser incluidas en un árbol generador mínimo.

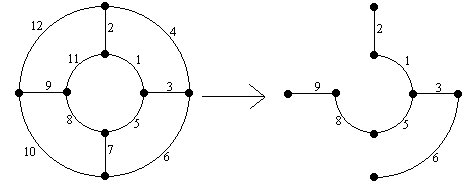
Ejemplo: