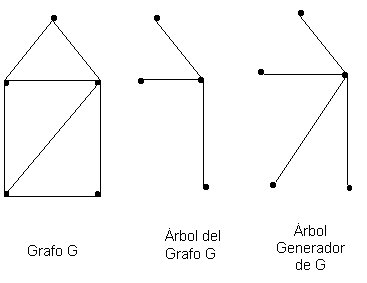
Sean G un grafo conexo donde los vértices representan edificios y las aristas túneles de conexión entre los edificios. Se quiere determinar un subconjunto de túneles que debieran mantenerse que pudiéramos alcanzar un edifico desde otro a través de estos túneles. También se desea determinar los subconjuntos de túneles que el ser obstruidos separarían a algunos edificios de otros (subconjunto de aristas de conexión y subconjunto de aristas de no conexión de un grafo).
Definición:
Un árbol de un grafo es un subgrafo del grafo que es un árbol.
Un árbol generador de un grafo conexo es un subgrafo generador que es
un árbol.
Ejemplo:

Definición:
Una rama de un árbol es una arista del grafo que es un árbol.
Una cuerda o enlace de un árbol es una arista del grafo que no está
en el árbol. El conjunto de cuerdas de un árbol se conoce como
el complemento del árbol.
Ejemplo:
Del grafo G, del ejemplo anterior, el siguiente grafo es su complemento.
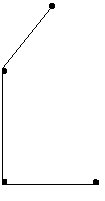
Definición:
Un grafo conexo siempre contiene un árbol generador. Si un grafo es conexo
y no contiene circuitos entonces es un árbol. Si el grafo contiene uno
o más circuitos, podemos eliminar una arista de los circuitos y aún
tener un subgrafo conexo.
Definición:
Un grafo generador es un subgrafo mínimo conexo de un grafo conexo en
el sentido de que a partir de un subgrafo conexo el cual no sea un árbol
generador, una o más de sus aristas pueden eliminarse, de manera que
el grafo resultante aún sea un subgrafo conexo y, por otra parte, ninguna
arista puede eliminarse de un árbol generador de manera que el subgrafo
resultante aún sea un subgrafo conexo.
Definición:
Para un grafo conexo con e aristas y v vértices, existen
v - 1 ramas en cualquier árbol generador. Entonces, en relación
con cualquier árbol generador, existen e - v + 1 cuerdas.
Definición:
Un conjunto de corte es un conjunto (mínimo) de aristas en un grafo tal
que la eliminación del conjunto incrementa el número de componentes
conexas en el subgrafo restante, en tanto que la eliminación de cualquier
subconjunto propio de este no lo haría. De esto se tiene que en un grafo
conexo, la eliminación de un conjunto de corte divide el grafo con dos
partes. Este sugiere una forma alternativa de definido en conjunto de corte.
Definición:
Si los vértices de una componente conexa a un grafo se divide en dos
subconjuntos, de manera que cada dos vértices en cada subconjunto estén
conectados por un paseo que sólo atraviesa vértices en tal subconjunto,
entonces el conjunto de aristas que una los vértices de los dos subconjuntos
es un conjunto de corte.
Ejemplo:
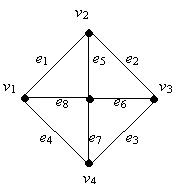
Para este grafo el conjunto de aristas {e1, e5, e6, e7, e4} es un conjunto de corte, ya que su eliminación dejará un subgrafo no conexo como el siguiente.
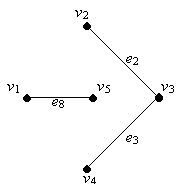
Este grafo es isomorfo al grafo anterior y se ve más claramente la división de los vértices para obtener un subgrafo no conexo como el obtenido anteriormente.
