Definición:
Diremos que un conjunto de sucesiones es un código de prefijos si no existe una sucesión del conjunto que sea un prefijo de otra sucesión del conjunto.

Ejemplo:
El conjunto {000, 001, 01, 10, 11} es un código de prefijos.
El conjunto {1, 00, 01, 000, 0001} no lo es un código de prefijos.

A partir de un árbol binario dado, podemos obtener directamente un código de prefijos binario. Primero etiquetamos las aristas con 0 y 1. Las aristas que corresponden al subárbol izquierdo se etiquetan con 0 y las derechas con 1.

Ejemplo:
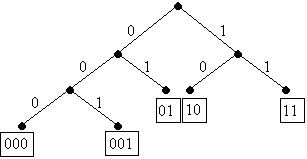
Sea el siguiente árbol binario:

Es evidente que el conjunto de sucesiones asignadas a las hojas de cualquier árbol binario es un código de prefijos. El código de prefijos obtenido es {000, 001, 01, 10, 11}.

También podemos construir a partir de un código de prefijos un árbol binario.

Ejemplo:
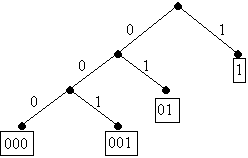
Tenemos el código de prefijos {001, 000, 01, 1} con el cual obtenemos el siguiente árbol binario de altura 3:

Ejemplo práctico:
Al almacenar o transmitir grandes cantidades de texto, frecuentemente conviene buscar la forma de comprimirlo en el menor número posible de bits. E l tiempo necesario para transmitir cierto mensaje es proporcional a su número de bits. Al comprimir los datos a enviar, puede reducirse el tiempo de transmisión. Además, los datos comprimidos necesitan menos bits para su almacenamiento.

Una manera de hacerlo es eliminar la restricción de que todos los códigos de caracteres deben tener la misma longitud. Si en un idioma los códigos de letras comunes como "e" y "t" fueran mas cortos que los códigos de los menos comunes como "x" y "z", disminuiría el número de bits totales necesarios para almacenar o transmitir el texto. Dicho esquema de codificación se llama código dependiente de frecuencia o código Huffman, basado precisamente en los prefijos codificados. Al utilizar este método de codificación para cualquier aplicación particular, han de conocerse las frecuencias a priori a cada carácter.

El primer paso para construir el código es escribir la probabilidad de cada carácter debajo de este. El orden en que se acomodan los caracteres no importa y puede combinarse durante la construcción para mayor legibilidad. Después se buscan las dos probabilidades más pequeñas y se añade una nueva probabilidad igual a la suma de aquellas. Las dos probabilidades se marcan para no ser utilizadas de nuevo y se trazan dos aristas que unan a la nueva probabilidad con las que le dieron origen. Este proceso se repite una y otra vez hasta que solo quede una probabilidad sin marcar, que será igual a 1.00.

Construiremos el código Huffman para una supuesta trasmisión para los dígitos 0,...,9 basados en las probabilidades siguientes:

El árbol resultante es el siguiente:

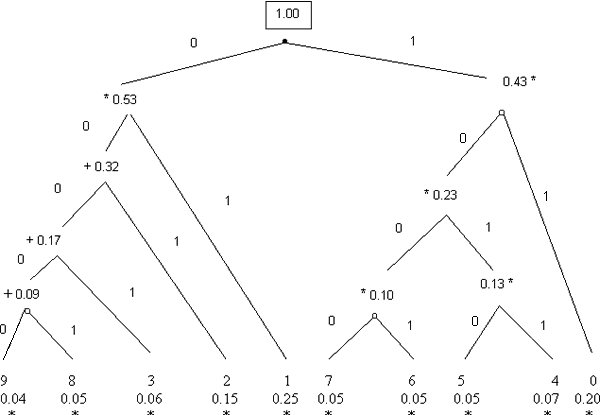
El código Huffman resultante para cada dígito es: