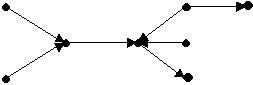
Este es un árbol dirigido
Definición:
Diremos que un grafo dirigido es un árbol dirigido
si se convierte en un árbol cuando se ignoran las direcciones de sus
aristas.

Este es un árbol dirigido
Definición:
Un árbol dirigido es un árbol enraizado si existe exactamente
un vértice cuyo grado de entrada sea 0 y los grados de entrada de los
otros vértices sea 1. El vértice con grado de entrada 0 es llamado
raíz del árbol enraizado.
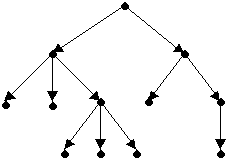
Árbol enraizado
Definición:
En un árbol enraizado, un vértice cuyo grado de salida sea 0 se
llama nodo hoja o nodo terminal, y un vértice cuyo grado de salidas sea
diferente de 0 se llama nodo rama o nodo interno.
Ejemplo:
Sea el siguiente árbol dirigido

Entonces:
Los nodos a, b, c, f, h son nodos rama y los nodos d, e, g, i, j, k, l son nodos
hoja.
Definición:
Sea a un nodo rama en un árbol enraizado. Diremos que un vértice
b es un hijo de a si existe una arista de a a b. Además se dice que el
vértice a es el padre de b. Dos vértices son hermanos si son hijos
del mismo vértice. Diremos que un vértice c es un descendiente
de a si existe un paseo dirigido de a a c. Además, se dice a es un ancestro
c.
Ejemplo:
Sea el siguiente árbol dirigido
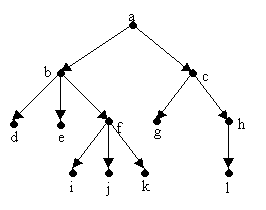
Entonces:
| b, c son hijos de a d, e, f son hijos de b g, h son hijos de c i, j, k son hijos de f l es hijo de h |
a es padre de b, c b es padre de d, e, f c es padre de g, h f es padre de i, j, k h es padre de l |
b, c son hermanos d, e, f son hermanos g, h son hermanos i, j, k son hermanos l no tiene hermanos |
| b, ,c, d, e, f, g, h, i, j, k, l son descendientes
de a d, e, f, i, j, k son descendientes de b i, j, k son descendientes de f g, h, l son descendientes de c l es descendiente de h |
a es ancestro de b ,c, d, e, f, g, h, i,
j, k, l b es ancestro de d, e, f, i, j, k f es ancestro de i, j, k c es ancestro de g, h, l h es ancestro de l |
Definición:
Sea a un nodo rama en un árbol T. Por el subárbol con raíz
a entendemos el subgrafo T'= (V', E') de T tal que V' contiene a a y a todas
sus descendientes y E' contiene las aristas de todos los paseos dirigidos que
surjan de a. Por un subárbol de a entendemos un subárbol que tiene
a a como raíz.
Ejemplo:
Sea el siguiente árbol dirigido T
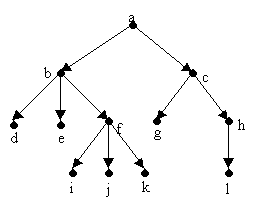
Entonces
|
i) |
ii) |
iii) |
i), ii) y iii) son subárboles de T cuyas raíces
son b, f y c respectivamente.
Observación:
Cuando se trace un árbol enraizado, si nos apegamos a la convención
de colocar los hijos de un nodo rama bajo este, las flechas de las aristas pueden
omitirse, debido a que puede entenderse a que apuntan hacia abajo.
Ejemplo:

Ahora veamos los siguientes árboles:
|
i) |
ii) |
A pesar de que los árboles i) y ii) enraizados son isomorfos podrían represéntanos dos situaciones completamente diferentes. Esto motiva a la siguiente definición de un árbol ordenado, lo cual permitirá referirnos sin ambigüedades a cada uno de los subárboles de un nodo rama. Veámosla
Definición:
Un árbol ordenado es un árbol enraizado con las aristas incidentes
de cada nodo rama, etiquetadas con los enteros 1, 2, ..., i, ... por
lo tanto, los subárboles de un nodo rama pueden ser referidos como el
primero, el segundo, ..., y el i-ésimo subárboles del nodo
rama y corresponden a las aristas incidentes desde el nodo, que pueden se enteros
no consecutivos.
Ahora supongamos que los árboles anteriores se etiquetan como se muestran
a continuación:
|
i) |
ii) |
Definición:
Dos árboles ordenados son isomorfos si existe una correspondencia uno
a uno entre sus vértices y sus aristas, la cual conserva la relación
de correspondencia, y si las etiquetas de las aristas correspondientes coinciden.
Así los árboles ordenados i) y ii) no son isomorfos.
Definición:
Un árbol ordenado en el cual cada nodo rama tiene a lo más m
hijos es llamado árbol m-ario. Diremos que un árbol m-ario
es regular si cada unas de sus ramas tiene exactamente m hijos. Una clase
importante de árboles m-arios son los llamados árboles
binarios. En los árboles binarios en lugar de referirnos al primero o
al segundo subárbol de un nodo rama, a menudo nos referimos al subárbol
izquierdo o al subárbol derecho del nodo.
Ejemplo:
|
Árbol ternario regular |
Árbol ternario |