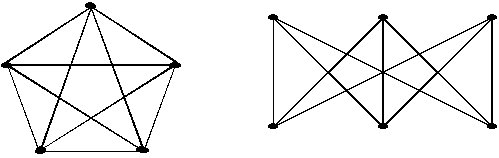
Este tipo de grafos, además de aparecer con mucha frecuencia también cuentan con muchas propiedades interesante. Se analizarán algunas de las más importantes.

Definición:
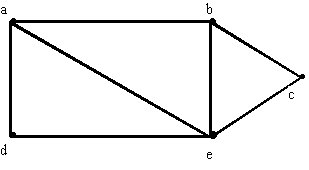
Diremos que un grafo es aplanable si puede ser dibujado sobre un plano de tal manera tal que ninguna arista se cruce con otra excepto, desde luego, en los vértices comunes. El siguiente es un grafo aplanable:

Ejemplo:
La siguiente figura es un grafo no aplanable que a decir verdad corresponde al problema de determinar si es posible conectar las casas 1, 2, 3 a los servicios de Luz, Agua y Drenaje, de tal manera que no haya 2 líneas de conexión que se crucen una con la otra.

Definición:
Una región (o cara) de un grafo aplanable se define como una área del plano que está acotada por aristas y no pude continuar dividiéndose subáreas.

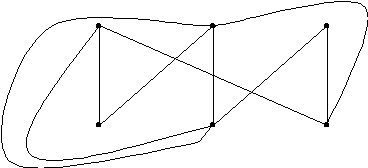
Ejemplo:
El siguiente grafo tiene 5 regiones que son:

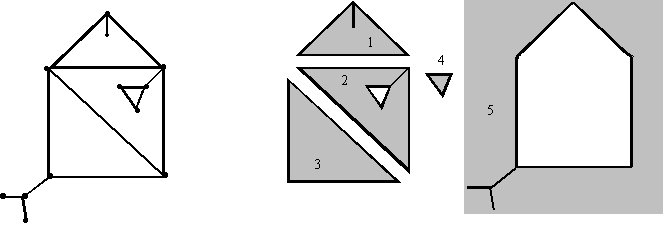
Definición:
Diremos que una región es infinita si su área es infinita y se dice que es finita, si su área es finita. En un grafo aplanable se tienen exactamente una región infinita.

Tenemos el siguiente resultado:

v e + r = 2

donde v, e y r son el numero de vértices, aristas y regiones respectivamente. Esta ecuación se conoce como la Formula de Euler para grafos aplanables. Sin excepción alguna todos los grafos aplanables conexos deben satisfacer la formula de Euler.

En cualquier grafo aplanable lineal conexo que no tenga lazos y que tenga 2 o mas aristas se cumple la siguiente desigualdad:

e 3v 6

Debido a que el grafo es lineal cada región es acotada por 3 o más aristas por lo tanto el número es mayor o igual que 3r. en la frontera a lo largo de 2 regiones, el numero total es igual o menor a 2e así tenemos:

2e 3r

ó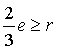

De acuerdo a la fórmula de Euler, tenemos que:

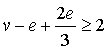ó

3v - 6 e

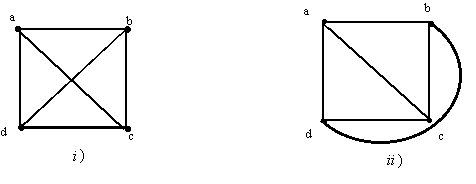
Es evidente que la planaridad de un grafo no se ve afectada si una arista es dividida en dos arista por la inserción de un vértice de grado 2 como i) o si 2 aristas se combinan en una sola arista al eliminar este vértice como en ii)

i)	ii)

Definición:
Dos grafos G₁ y G₂ son isomorfos bajo vértices de grado 2, si son isomorfos ó si pueden transformarse en grafos isomorfos mediante repeticiones de inserciones y/o eliminaciones de vértices de grado 2 como en i) y i i).

Ejemplo:
Los siguientes grafos son isomorfos bajo vértices de grado 2.

Teorema de Kuratoswki
Un grafo es aplanable si y solo si no contiene cualquier subgrafo que sea isomorfo bajo vértices de grado 2 a cualquier de los siguientes grafos, que son llamados de Kuratowski