Definición:
Dos grafos G₁ y G₂ son isomorfos si existe una función biyectiva f entre los vértices de G₁ y G₂, y una función biyectiva g entre lados de G₁ y G₂ tales que un lado e es incidente a v y w en G1 si solo si el lado g(e) es incidente a los vértices f (v) y f (w) en G₂. Al par de funciones f y g se le denomina isomorfismo.

Ejemplo:
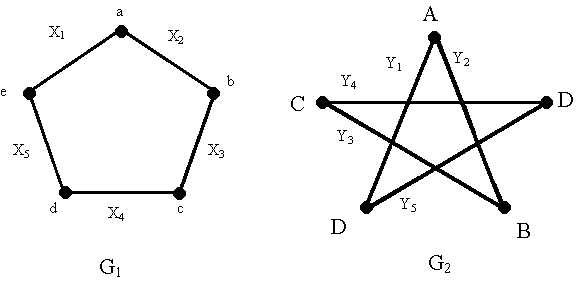
Sean los siguientes grafos G₁ y G₂

Un isomorfismo para los grafos anteriores G₁ y G₂ esta definido por:
f (a) = A
f (b) = B
f (c) = C
f (d) = D
f (e) = E

y g(X_i) = Y_i, i = 1, ... , 5

Los grafos G₁ y G₂ son isomorfos si y solo si para alguna ordenación de vértices y lados sus matrices de incidencia son iguales. Veamos las matrices de incidencia de los grafos anteriores:

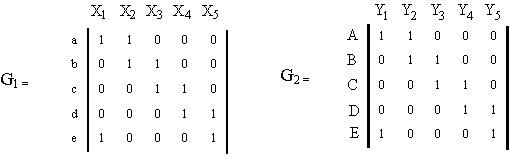
Ejercicios:
Verificar si los siguientes pares de grafos son isomorfos.

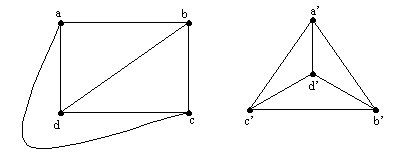
a)

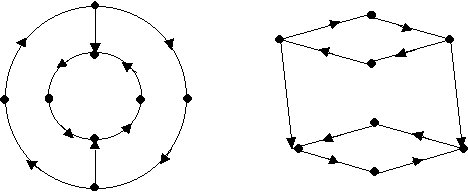
b)