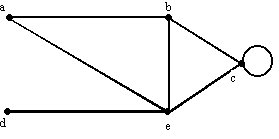
Hasta ahora se ha visto como representar un grafo mediante un esquema. Algunas veces, por ejemplo, cuando se desea analizar un grafo en una computadora, se necesita una presentación más formal. Un primer método de representación de un grafo lo constituye la matriz de adyacencia.

Para obtener la matriz de adyacencia de un grafo, se selecciona un orden arbitrario de vértices, supongamos que nuestro grafo tiene 5 vértices: a, b, c, d y e. A continuación, se le asignan a las filas y a las columnas de la matriz el mismo orden dado a los vértices. Un elemento de una matriz es 1 si los vértices correspondientes a la fila (renglón) y a la columna de dicho elemento están unidos por un lado (arista), y 0 en caso contrario.

Ejemplo:
La matriz de adyacencia para este grafo es:

A =

La matriz de adyacencia permite representar lazos, no permite representar lados paralelos. Si el grafo no tiene lados paralelos ni lazos, se puede obtener la valencia de un vértice sumando la fila o la columna correspondiente

Ejemplo:

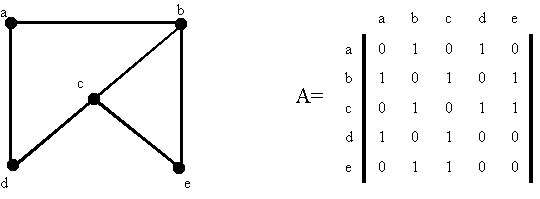
La matriz de adyacencia no es una manera muy eficaz de representar un grafo. Como es simétrica con respecto a la diagonal la información, exceptuando la contenida en la diagonal, aparece dos veces.

Otra representación útil de un grafo es la conocida como matriz de incidencia como se puede ver en el siguiente grafo:

Se le asigna a las filas las marcas correspondientes a los vértices y a las columnas las correspondientes a los lados. El elemento que corresponde a la fila y a la columna e es 1 si es incidente en algún vértice v y es 0 en cualquier otro caso.

Una columna semejante a e₇ representa un lazo.

La matriz de incidencia permite representar lados paralelos y lazos simultáneamente.

Un grafo sin lazos en cada columna tiene dos cifras 1 y la suma de cada fila da la valencia del vértice correspondiente.