5.4.2 PASES Y CIRCUITOS DE HAMILTON

Un problema similar a la determinación de un paseo o un circuito de Euler, es el de determinar un paseo o circuito que pasa a través de un vértice en un grafo una y sólo una vez.

Definición:
Un paseo hamiltoniano es un paseo que pasa a través de cada un de los vértices exactamente una vez.

Definición:
Un ccircuito hamiltoniano como un paseo circuito que pasa a través de cada un de los vértices exactamente una vez.

NOTA:
No se conoce ninguna condición necesaria y suficiente para demostrar la existencia de un paseo o un circulo de Hamilton en un grafo.

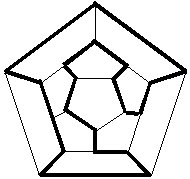
Ejemplo:
Encuentre un circuito de Hamilton en el siguiente grafo:

 

El siguiente es un resultado general sobre la existencia de paseos o circuitos hamiltonianos.

Sea G un grafo no dirigido de tipo lineal de n vértices. Si la suma de los grados para cada par de vértices de G es n - 1 o mayor, entonces existe un paseo de Hamilton en G.

Ejemplo:

La consideración anterior es una condición suficiente pero no necesaria para la existencia de un paseo hamiltoniano en un grafo.