Definición:
Un paseo de Euler (Euleriano) es un camino que incluye todos los lados - y por lo tanto todos los vértices - de un grafo dado, una y solo una vez.

Definición:
Un circuito de Euler (Euleriano) es un circuito que incluye todos los lados - y por lo tanto todos los vértices - de un grafo dadouna y solo una vez.

Condiciones para saber si un grafo dado tiene un paseo o circuito de Euler.

1) Un grafo no dirigido G tiene un paseo de Euler si y solo si tiene cero o dos vértices de valencia impar.

2) Si un grafo no dirigido G tiene un circuito de Euler entonces todo vértice de G tiene valencia par, además de ser conexo.

3) Si G es un grafo no dirigido con vértices {v₁, v₂, ... , v_n} y la suma

(v₁), (v₂), ... , (v_n)

es par, entonces el grafo tiene un circuito de Euler.

4) Un grafo G tiene un camino de Euler de v w si y solo si v y w son los únicos vértices de valencia impar.

Ejemplo:
Verificar si los siguientes grafos no dirigidos tienen un paseo o circuito de Euler.

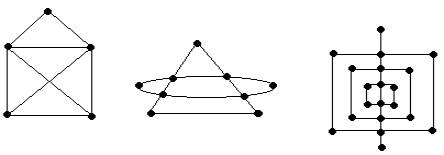Paseo de Euler	SI	Si	Si
Circuito de Euler	No	Si	No

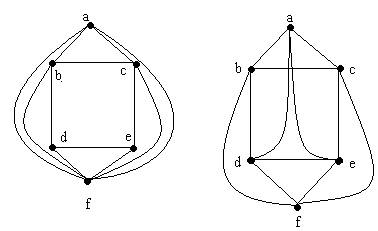Paseo de Euler	Si	Si
Circuito de Euler	No	Si

Los resultados obtenidos para grafos no dirigidos pueden extenderse de inmediato para grafos dirigidos.

Definición:
En un grafo dirigido el grado o valencia de entrada de un vértice es el numero de lados incidentes hacia este y el grado de salida es el numero de lados que son incidentes desde este.

Definición:
Un grafo dirigido tiene un circuito de Euler si y solo si es conexo y el grado de entrada de cualquier vértice es igual a su salida.

Definición:
Un grafo dirigido tiene un paseo de Euler si y solo si es conexo y el grado de entrada de cualquier vértice es igual a su grado de salida con la posible excepción de solo dos vértices. Para estos dos vértices el grado de entrada de uno de ellos es mayor que su grado de salida y el grado de entrada del otro es menor que su grado de salida.

Ejemplo:
Verificar si los siguientes grafos dirigidos tienen un paseo o circuito de Euler.

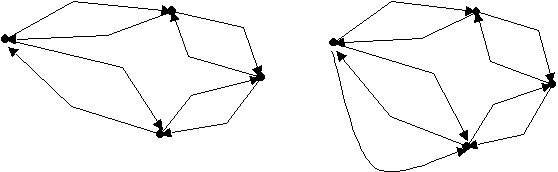Paseo de Euler	Si	Si
Circuito de Euler	Si	No