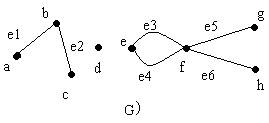
Con frecuencia se abrevia la asociación de lados
{(v0, v1), (v1, v2 ), ...., (vn-1 , vn )}
como
(v0, v1, v2, ... , vn)
Ejemplo:
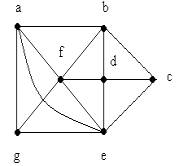
Sea el siguiente grafo G

La sucesión de lados {(a, b), (b, f ), (f, g), (g, e)} se puede representar como (a, b, f, g, e)
Definición:
Sea G un grafo y sean v y w vértices de G.
a) Un camino de longitud n de v a w es una sucesión de lados que de v a w, la cual tiene n lados distintos entre si.
b) Un camino simple de longitud n de v a w es de la forma (v0, v1, v2, ... , vn) donde v0 = v y vn = w y v0, v1, v2, ... , vn son distintos entre si.
c) Un circuito o ciclo es un camino de v a v.
d) Un circuito simple es un circuito de la forma (v0,
v1, v2, ... , vn) donde
v0 = v y vn = vn-1
son distintos entre si.
Ejemplo:
Sea el siguiente grafo no dirigido G.
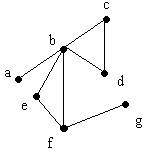
G
Basándose en el grafo anterior llénese la siguiente
tabla:
| Sucesión de lados | Camino | Camino simple | Circuito | Circuito simple |
| (a, b, c, b, a) | NO | NO | NO | NO |
| (f, e, b, d, c, b, a,) | SI | NO | NO | NO |
| (f, e, b, d) | SI | SI | NO | NO |
| (b, f, e, b, d, c, b) | SI | NO | SI | NO |
| (e, f, b, e) | SI | NO | SI | SI |
Definición:
Se dice que un grafo G es conexo si, para cualquier par de vértices (v,
w) distintos entre si, existe un camino de v a w.
Ejemplo:
El siguiente grafo es no conexo