Definición:
Un grafo (grafo no dirigido) G consta de un conjunto V de vértices o nodos y un conjunto E de lados, (ramas o aristas) tales que cada lado e E esta asociado a un par no ordenado de vértices.

Si un lado e esta asociado a un único par de vértices v y w se escribe e = (v, w) o también se escribe e = (w, v).

NOTA:
En este contexto (v, w) denota un lado de un grafo no dirigido y no un par ordenado de números.

Definición:
Un grafo dirigido (o dígrafo) G consta de un conjunto V de vértices y un conjunto E de lados, tal que e E esta asociado a un par ordenado único de vértices v y w y se escribe e = (v, w).

Definición:
Se dice que un lado e = (v, w) de un grafo (dirigido o no dirigido) es incidente en v y w. Se dice que los vértices v y w son incidentes en e y también que los vértices son adyacentes.

Si G es un grafo (dirigido o no dirigido) con un conjunto de vértices V y un conjunto de lados E, se escribe G = (V, E).

Ejemplo:

G

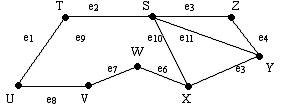
Este grafo G consta de un conjunto V de vértices

V = {S, T, U, V, W, X, Y, Z}

y el conjunto de lados

E = {e1, e2, e3, .... , e11 }.

El lado e1 esta asociado con el par no ordenado {T, U}, el lado e10 esta asociado al par no ordenado {S, X}. El lado e1 se denota por (U, T) o bien (T, U). El lado e4 es incidente en los vértices Y y Z por lo que Y y Z son vértices adyacentes.

Ejemplo:

G

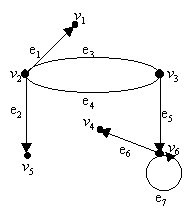
En este dígrafo los lados dirigidos están indicados por flechas. El lado e₁ esta asociado al par ordenado de vértices (v₂ , v₁) por lo que se escribe e₁ = (v₂ , v1) y el lado e₇ con el par ordenado (v₆, v₆), por lo que se escribe e₇ = (v₆, v₆).

Ejemplo:
Consideremos ahora el siguiente grafo:

G

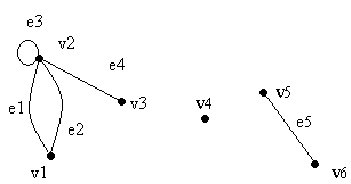
Cuando dos lados distintos están relacionados con el mismo par de vértices se llaman lados paralelos, como e₁ y e₂ que están asociados con el par no ordenado de vértices {v₁ , v₂}. Un lado de la forma (v, v) que inicia y termina en el mismo vértice se llama lazo, como ocurre en e₃ = (v₂, v₂). En el grafo G ningún lado es incidente a v₄, un grafo que no tiene lazos ni lados paralelos recibe el nombre de grafo simple.

Ejemplo:

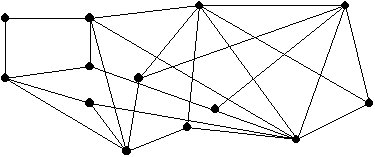
Grafo simple

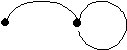
Grafo no simple

Definición:
Un grafo completo de n vértices, que se denota K_n, es el grafo simple con n vértices en el cual existe una arista entre cada par de vértices distintos.

Ejemplo:

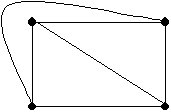
Grafo completo K₄

Ejemplo:
Problema de los puentes de Köningsberg.

Dos islas que se encuentran en el río Pregel en Köningsberg (antes Prusia Oriental, llamado ahora Kaliningrado) están conectadas entre si y con la margen del río por puentes como se indica en la siguiente figura:

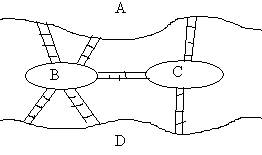
El problema consiste en partir desde cualquier lugar (A, B, C, o D), seguir caminando y pasar por cada uno de los puentes una sola vez y luego volver al punto de partida.

A un recorrido de este tipo se llama "circuito de Euler". Tal recorrido puede representarse mediante un grafo como sigue:

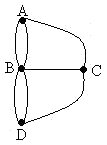
La solución puede obtenerse fácilmente utilizando el concepto de valencia de un vértice.

Definición:
La valencia (o grado) de un vértice v se denota (v) y es numero de datos incidentes en v.

Ejemplo:
Del grafo anterior tenemos que:

(A) = 3
(B) = 5
(C) = 3
(D) = 3

Más adelante se demostrará que el Problema de los puentes de Köningsberg no tiene solución.

Un problema similar al de encontrar un circuito de Euler en un grafo es el obtener un circuito Hamiltoniano. Un circuito de Hamilton en un grafo G es un camino que comienza y termina en el mismo vértice, pasando exactamente una vez por cada vértice.

Ejemplo:

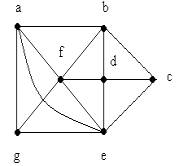
El camino (a, b, c, d, e, f, g, a) o (a, b, c, d, f, e, g, a) es un circuito Hamiltoniano. Este grafo no tiene circuito de Euler. En un circuito de Euler se pasa por cada lado exactamente una vez, en tanto que en un circuito de Hamilton se pasa por cada vértice exactamente una vez.

Definición:
Sea un grafo G = (V, E), diremos que un grafo G' = (V', E') es un subgrafo de G si E' E y V' V tal que los lados de E' sean incidentes en los vértice de V'.

Definición:
El complemento de un subgrafo G' = (V', E') con respecto a un grafo G es otro grafo G'' = (V'', E'') tal que E'' = E - E' ó E = E'+ E'' y V'' contiene a los vértices con los cuales E'' son incidentes.

Ejemplo:
Consideremos los siguiente grafos:

Sea en i) G = (V, E), donde V = {a, b, c, d, e, f, g, h} y E = {e1, e2, e3, e4 .... , e12}

Sea en ii) G' = (V', E'), donde V' = {b, c, d, e, f, g, h} y E' = {e4, e5, e7, e8, e11, e12}, además se tiene que E' E y V' V tal que los lados de E'sean incidentes en los vértice de V', por lo que G' es un subgrafo de G.

Además en iii) G'' = (V'', E''), donde V'' = {a, b, c, d, f, g, h} y E'' = {e1, e2, e3, e6, e9, e10}, además E'' = E - E' y V''contiene a los vértices con los cuales E'' son incidentes, por lo que G'' es el complemento del subgrafo de G'.

Definición:
Se dice que G' es un subgrafo generador si contiene todos los vértices de G

Ejemplo:
Sea el siguiente subgrafo del grafo i) del ejemplo anterior.

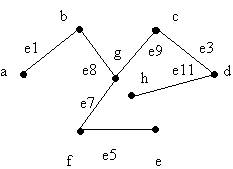
Se tiene que: V' = {a, b, c, d, e, f, g, h} y E' = {e1, e3, e5, e7, e8, e9, e11} y como V' contiene todos los vértices de G, entonces G' es un subgrafo generador de G.