y
que n - (n - r ) = r se tiene la siguiente identidadIdentidades básicas
Puesto que y
que n - (n - r ) = r se tiene la siguiente identidad
Otra identidad importantes es:
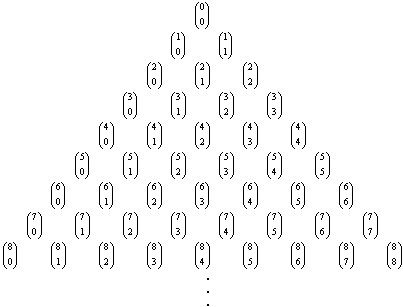
Otra identidad muy útil es
Utilizando la identidad anterior para obtenr la suma 1 + 2 + ... + n
Es posible expresar
se llaman coeficientes binomiales, pues aparecen en el desarroloo del binomio
(a + b) elevado a alguna potencia.
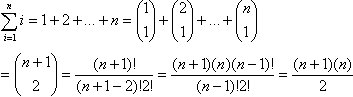
Este teormea proporciona una fórmula para los coeficientes del desarrollo (a + b)n. Ya que:
Si n = 2
(a + b)2 = (a + b)(a + b) = aa + ab + ba + bb = a2 + 2ab + b2.
Un término de la forma 
proviene de tomar a de n - k factores, y b de k
factores. Pero puede hacerse de 
formas, pues cuenta el número
de formas de seleccionar k los n objetos dados. Por lo tanto
aparece veces. Luego
Ahora enunciemos el Teorema del binomio.
Si a y b son números reales
y n 
+,
entonces
Ejemplo:
Tomando n = 3 tenemos que:
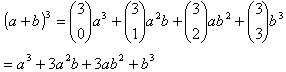
Triángulo de Pascal
También puden expresarse los coeficientes
binomiales mediante un arreglo triangular conocido como Triángulo de
Pascal. Los dos lados superioes están formados por númeors 1,
y cuaiquier valor interior es la suma de los dos números que están
por encima y a los lados del él, es decir:
o bien, espresado en forma de coeficientes binomiales tenemos que:
