El principio de exclusión-inclusión nos dirá el tamaño de una unión en términos de varias intersecciones. Sean A1, A2, . . . , An conjuntos finitos. Para n = 2 la regla de la unión afirma que:
|A1 ![]() A2| = |A1| + |A2|
A2| = |A1| + |A2| ![]() |A1
|A1 ![]() A2|
A2|
para n = 3 el principio de exclusión-inclusión afirma que:
| | A1 |
| A1 | + | A2
| + | A3 | |
| | A1 |
y para n = 4
| | A1 |
| A1 | + | A2
| + | A3 | + | A4 | |
| | A1 |
|
| | A3 |
|
| | A1 |
|
| | A1 |
Definición:
Para calcular el tamaño de A1
![]() A2
A2
![]() . . .
. . . ![]() An debemos calcular el tamaño de todas las posibles
intersecciones de conjuntos {A1, A2, . .
. , An} sumar los resultados obtenidos al intersectar
un numero impar de conjuntos y restar los resultados obtenidos al intersectar
un número par de conjuntos.
An debemos calcular el tamaño de todas las posibles
intersecciones de conjuntos {A1, A2, . .
. , An} sumar los resultados obtenidos al intersectar
un numero impar de conjuntos y restar los resultados obtenidos al intersectar
un número par de conjuntos.
Los términos "exclusión-inclusión" indican que hay que incluir o sumar los tamaños de los conjuntos, después excluir o restar los tamaños de las intersecciones de dos conjuntos, luego incluir o sumar los tamaños de todas las intersecciones de tres conjuntos, etc, es decir:
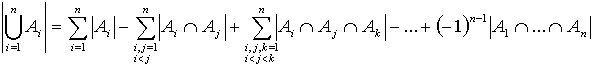
Ejemplos:
a) ¿Cuántos números hay del
50 al 12,000, excluyendo los múltiplos de 3 y de 5?. Es fácil
equivocarse. Intentemos organizarnos: Del 50 al 12,000 hay 12,000 - 50 + 1 =
11,951 numeros. Tendríamos que restar de esta cantidad, los que son multiplos
de 3 o de 5.
Si llamamos N3 al conjunto de los multiplos de 3 entre el 50 y el 12,000 y N5 al de los multiplos de 5, y si con |A| indicamos la cantidad de elementos que tiene A, la solucion a nuestro problema es
11,951 - |N3 ![]() N5|.
N5|.
Ahora: |N3 ![]() N5| = |N3| + |N5| - |N3
N5| = |N3| + |N5| - |N3 ![]() N5| .
N5| .
Notemos que ser multiplo de 3 y de 5 es lo mismo que ser multiplo
de 15, entonces se N15, al conjunto de lus multiplos de 15 entre 50 y 12,000.
Además que |Nk| ![]() (12,000
/ k) - (49 / k), recordar que la división es entera. Entonces
para obtener |N3| = (12,000 / 3) - (50 / 3) = 4,000 - 16 = 3,984. Para |N5|
= (12,000 / 5 ) - (49 / 5) = 2,400 - 9 = 2,391. Y para |N15| = 800 - 3 = 797.
(12,000
/ k) - (49 / k), recordar que la división es entera. Entonces
para obtener |N3| = (12,000 / 3) - (50 / 3) = 4,000 - 16 = 3,984. Para |N5|
= (12,000 / 5 ) - (49 / 5) = 2,400 - 9 = 2,391. Y para |N15| = 800 - 3 = 797.
Así, | N3 ![]() N5 | = 3,984 + 2,391 - 797 = 5,578, y la cantidad buscada es 11,951 - 5,578
= 6,373.
N5 | = 3,984 + 2,391 - 797 = 5,578, y la cantidad buscada es 11,951 - 5,578
= 6,373.
b) Contemos el número de enteros en S = {1, 2,
3, ..., 2000} que son divisibles por 9, 11, 13 ó 15. Para cada k
![]()
![]() +
hacemos |Dk| = {n
+
hacemos |Dk| = {n ![]() S | n es divisible por k} y buscamos |D9
S | n es divisible por k} y buscamos |D9 ![]() D11
D11 ![]() D13
D13 ![]() D15|. Notese que |Dk|
D15|. Notese que |Dk| ![]() (2000
/ k), división entera. Por lo tanto
(2000
/ k), división entera. Por lo tanto
|D9| = 222
|D11| = 181
|D13| = 153
|D15| = 133
|D9 ![]() D11| = |D99|
= 20
D11| = |D99|
= 20
|D9 ![]() D13| = |D117|
= 17
D13| = |D117|
= 17
|D9 ![]() D15| = |D45|
= 44
D15| = |D45|
= 44
|D11 ![]() D13| = |D143|
= 13
D13| = |D143|
= 13
|D11 ![]() D15| = |D165|
= 12
D15| = |D165|
= 12
|D13 ![]() D15| = |D195|
= 10
D15| = |D195|
= 10
|D9 ![]() D11
D11 ![]() D13| = |D1287| = 1
D13| = |D1287| = 1
|D9 ![]() D11
D11 ![]() D15| = |D495| = 4
D15| = |D495| = 4
|D9 ![]() D13
D13 ![]() D15| = |D585| = 3
D15| = |D585| = 3
|D11 ![]() D13
D13 ![]() D15| = |D2145| = 0
D15| = |D2145| = 0
|D9 ![]() D11
D11 ![]() D13
D13 ![]() D15| = |D6435|
= 0
D15| = |D6435|
= 0
Observese, por ejemplo, que D9 ![]() D15 = D45 y no D135, ya que el mcm(9,15) = 45.
D15 = D45 y no D135, ya que el mcm(9,15) = 45.
Ahora por el principio de exclusión-inclusión tenemos que:
| |D9 |
222 + 181 + 153 + 133 - |
| (20 + 17 + 44 + 13 + 12 + 10) + | |
| (1 + 4 + 3 + 0) - 0 = 581 |
c) Supongamos que tenemos seis computadoras con las siguientes especificaciones:
| Computadora | Quemador (A1) | Procesarod PIV (A2) | Pantalla Plana (A3) |
| I | SI | SI | NO |
| II | SI | SI | SI |
| III | NO | NO | NO |
| IV | NO | SI | SI |
| V | NO | SI | NO |
| VI | NO | SI | SI |
¿Cuántas computadoras tienen uno o más de los 3 tipos de hardware?
| A1 | = 2
| A2 | = 5
| A3 | = 3
| A1 ![]() A2 | = 2
A2 | = 2
| A1 ![]() A3 | = 1
A3 | = 1
| A2 ![]() A3 | = 3
A3 | = 3
| A1 ![]() A2
A2 ![]() A3 | = 1
A3 | = 1
En consecuencia por el principio de exclusión-inclusión
| A1 ![]() A2
A2 ![]() A3 | = 2 + 5 + 3
- 2 - 1 - 3 + 1 = 5
A3 | = 2 + 5 + 3
- 2 - 1 - 3 + 1 = 5
computadoras que tienen uno o más tipos de hardware.
d) De 200 estudiantes 50 toman el curso de matemáticas discretas, 140 el curso de economía y 24 ambos. Como ambos cursos programaron exámenes para el día siguiente, sólo los estudiantes que no esten en ninguno de estos curso podrán ir a la fiesta de la noche. Se quiere ver cuántos estudiantes iran a la fiesta.
Sea A1 = Estudiantes de matemáticas discretas y A2 = Estudiantes de economía. Por el principio de exclusión-inclusión ssse tiene que:
| A1 ![]() A2 | = 50 + 140 -24 = 166 estudiantes que toman uno o ambos cursos. En consecuencia
2002 - 166 = 34 estudiantes son los que iran a dicha fiesta.
A2 | = 50 + 140 -24 = 166 estudiantes que toman uno o ambos cursos. En consecuencia
2002 - 166 = 34 estudiantes son los que iran a dicha fiesta.
e) Determine el número de enteros positivos n tales
que 1 ![]() n
n
![]() 100 y n
no es divisible entre 2, 3 ó 5.
100 y n
no es divisible entre 2, 3 ó 5.
Sean:
D2 = Números divisibles entre 2
D3 = Números divisibles entre 3
D5 = Números divisibles entre 5
| D2 | = 50
| D3 | = 33
| A5 | = 20
| D2 ![]() D3 | = |
D6 | = 16
D3 | = |
D6 | = 16
| D2 ![]() D5 | = |
D10 | = 10
D5 | = |
D10 | = 10
| D3 ![]() D5 | = |
D15 | = 6
D5 | = |
D15 | = 6
| D2 ![]() D3
D3 ![]() D5 | = | D30 | = 3
D5 | = | D30 | = 3
Aplicando el principio de exclusión-inclusión tenemos que
| D2 ![]() D3
D3 ![]() D5 | = 50 + 33 +
20 - 16 - 10 - 6 + 3 = 74
D5 | = 50 + 33 +
20 - 16 - 10 - 6 + 3 = 74
Por lo tanto 100 - 7 4 = 26 número que no son divisble entre 2, 3, ó 5.
Estos número son 1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59, 61, 67, 71, 73, 77, 79, 83, 89, 91, 97