Teorema:
Supóngase que una sucesión S de n objetos tien n₁ objetos idénticos del tipo 1, n₂ objetos idénticos del tipo 2, . . . , n_t objetos idénticos del tipo t. Entonces el número de ordenaciones de S es:

Demostración:
Se asignan las posiciones de cada uno de los n objetos para crear un orden de S. Es posible asignar las posiciones de los n1 objetos del tipo 1 en C(n, n₁) formas. Una vbez realizada estas asignación, pueden asignarse las posiciones de los n₂ objetos del tipo 2 en C(n - n₁, n₂) maneras, etc. Por lo tanto

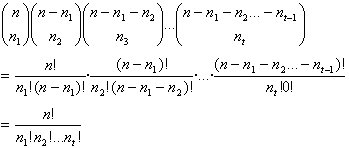
Ejemplos:
a) ¿De cuántas maneras es posible ordenar las siguiente letras ?

MISSISSIPPI

Debido a la repetición de algunas letras, la respuesta no es 11!, pero si un número menor a 11!.

Consideremos el problema de llenar 11 espacios en blanco

_ _ _ _ _ _ _ _ _ _ _

con las letras dadas. Hay maneras de escoger posiciones para las dos letras P. Una vez seleccionadas las dos P, existen manera de elegir posiciones para las cuatro S. Una vez seleccionas las posiciones para las letars S, hay maneras de escoger lugares para las letras I. Una vez realizadas estas elecciones, quesa un único lugar para ser llenado por la letra M. Por el Teorema anterior, directamente existen maneras de ordenar dichas letras.

b) De cuántos modos se pueden repartir ocho libros distintos entre tres estudiantes si Guillermo recibe cuatro libros, en tanto que Maria y Silvia reciben 2 cada una.

Sea G = Guillermo, S = Sofia y M = Maria.

Unos ejemplos de ordenación serian GGGGSSMM, GGGSMGMS, MMSSGGGG, etc.

Cada uno de estos ordenamientos determina una distribución de libros. Por lo que existen maneras de repartir los libros.

c) ¿De cuantas maneras pueden formarse tres comités distintos de un grupo de 20 personas, si los comités deben tner 3, 5 y 7 personas respectivamente?

La respuesta es

d) Una partida de Bridge es una partición ordenada de 52 cartas que comprende 4 conjuntos de 13 cartas cada uno. Por lo tanto hay partidas de Bridge.

e) ¿De cuántas maneras posibles pueden distribuirse 12 estudiantes en 3 grupos, con 4 estudiantes cada grupo, de manera que un grupo estudie un tema, el otro un tema diferente y el tercero otro diferente a los dos anteriores?

En total hay posibles maneras de distribuir a los estudiantes.

f) ¿De cuántas maneras pueden distribuirse 19 estudiantes en 5 grupos, 2 grupos de 5 y 3 grupos de 3, de manera que cada grupo estudie un tema distinto?

En total hay posibles maneras de distribuir a los estudiantes.

g) ¿De cuantás formas es posible hacer una partición de un conjunto de 100 elementos en 50 conujuntos diferentes de 2 elementos cada uno?

La respuest es 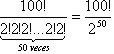formas posibles.

De forma más general puede enunciarse el mismo problema de la siguiente manera ¿De cuántas formas es posible hacer una partición de un conjunto conm 2n elementos en n conjuntos de 2 elelmentos cada uno?.

Entonces la respuesta es 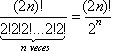formas posibles.

Teorema:
Si X es un conjunto que contiene n elementos, entonces el número de selecciones de r elementos, no ordenadas, con repeticiones permitidas y tomando del conjunto X es:

NOTA:
Es posible que r sea mayor que n cuando se permiten repeticiones.

Ejemplos:
a) Supongase que se tienen 3 pilas de pelotas rojas, azules y verdes y cada una contiene al menos 8 pelotas.
i) ¿De cuántos modos se pueden seleccionar 8 pelotas?
ii) ¿De cuántas maneras de pueden seleccionar 8 pelotas si se debe tener al menos una de cada color?

Por el Teorema anterior, el número de formas para elegir 8 pelotas es .

También se puede aplicar el Teorema para resolver la parte ii). Si se selecciona una pelota de cada color. Para completar la elección, deben escogerse 5 pelotas más. Esto se puede hacer de formas diferentes.

b)¿De cuántas maneras es posible colocar 10 canicas rojas en 5 bolsas?

La respuesta es maneras posibles.

c) ¿De cuántas maneras es posible seleccionar 10 monedas de un abasto ilimitado de monedas de cincuenta, cien, doscientos y quinientois pesos?

Entonces es posible seleccionar formas distintas.

d) De cuántas formas pueden distribuirse 12 libros idénticos de matemáticas discretas entre 4 estudiantes.

En total se pueden distribuir formas diferentes.

e) Cuántas soluciones enteras no negativas tiene la ecuación x₁ + x₂ +x₃ + x₄ = 29

Cada solución es equivalente a elegir 29 elementosm x_i del tipo i, i = 1, 2, 3, 4.El número solución es.

f) Una tienda ofrece 20 tipos de donas. Si suponemos que al menos hay una docena de cada tipo cuando entramos a la tienda, podemos elegir una docena de donas de opciones posibles.