Una permutación de objetos implica orden mientras que una combinación no toma el orden de los objetos considerados.

Definición:
Dado un conjunto que contiene n elementos distintos X = {x₁, x₂, .... x_n}

a) Una permutación de X es una ordenación de los n elementos x₁, x₂, .... x_n

b) Una permutación–r (ó r-permutación) de X donde r n, es una ordenación de un subconjunto de r elementos de X.

c) El numero de permutaciones-r de un subconjunto de n elementos distintos se denota P(n, r)

d) Una combinación-r (r-combinación) es una selección no ordenada de r elementos de X, es decir, un subconjunto de r elementos de X.

e) El numero de combinaciones-r de un conjunto de n elementos distintos y se denota C(n, r) ó bien .

Ejemplo:
Sea X = {a, b, c}
Algunas permutaciones de X son: abc, acb, bac
Algunas permutaciones-2 de X son: ab, ba, ca
Algunas combinaciones-2 de X son: {a, b}, {a, c}, {b, c}

Teorema:
El número de permutaciones-r de un conjunto de n objetos distintos es

P(n, r) =(n)(n -1)(n - 2)...(n - r +1)

La demostración es directa aplicando la regla b) del producto.

Por este teorema el número de permutaciones-2 de X = {a, b, c} es 6, las cuales son: ab, ac, ba, bc, ca, cb

También por este Teorema el número de permutaciones en un conjunto de n elementos es

P(n, n) = (n)(n -1)(n - 2)...(3)(2)(1) = n!

Observese que P(n, r)·(n - r)! = n!, por lo que

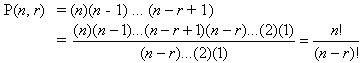
Ejemplos:
a) De cuántas maneras se puede seleccionar un presidente, un vicepresidente, un secretario y un tesorero entre un grupo de 10 personas .

La respuesta es P(10, 4) = 10!/(10 - 4)! = 5,040 ó bien 10 · 9 · 8 · 7 = 5,040 maneras diferentes.

b) ¿De cuántas formas puede formarse en una fila 7 mexicanos distintos y 5 gringos distintos si ninguna pareja de gringos puede estar junta?

Podemos formar a los mexicanos y a los gringos mediante un proceso de dos partes. Formando a los mexicanos y a los gringos. Los mexicanos pueden formarse de 7! = 5040 maneras. Una vez formados los mexicanos, como ninguna pareja de gringos puede estar junta, los gringos tienen 8 posiciones en las cuales formarse, es decir:

_ M₁ _ M₂ _ M₃ _ M4 _ M₅ _ M₆ _ M₇ _

Así los gringos pueden formarse de P(8, 5) = 6,720 maneras. Por la regla del producto tenemos que 5,040 · 6720 = 33'868,800 maneras diferentes de formarlos.

c) Se quieren colocar 3 pelotas de color rojo, azul y blanco en cajas numeradas con 1, 2, ... , 10. DEseamos conocer el número de maneras distintas en que las pelotas pueden ser colocadas en cajas, si cada caja es capaz de contener sólo una pelota.

Coloquemos las pelotas una a la vez, iniciando con la pelota roja, luego la azul y después la blanca. Puesto que la pelota roja puede colocarse en cualquiera de las 10 cajas, la azul en cualquiera de las 9 restantes y la blanca en cualquiera de las 8 restantes, el número total de maneras distintas de colocar estas pelotas es 10 · 9 · 8 = 720.

d) ¿De cuantas maneras pueden ser programados tres exámenes dentro de un periodo de 5 días, de modo que el mismo día no sean programados 2 exámenes?

Si consideramos que P(n, r) =(n)(n -1)(n - 2)...(n - r +1) = P(5, 3) = 5 · 4 · 3 = 60 maneras distintas de programas los exámenes.

e) ¿Cuántas permutaciones de las letras ABCDEF contienen la subcadena DEF?

Para garantizar la presencia del patrón DEF en la subcadena, estas 3 letras deben estar juntas y en ese orden. Las letras A, B y C pueden colocarse de manera arbitraria. Así es como tener 4 elementos diferentes, por lo que la respuesta es P(4, 4) = 4!.

f) ¿Cuántas permutaciones de las letras ABCDEF contiene las letras DEF juntas, pero en cualquier orden?

Se puede resolver este problema en dos pasos. Primero se elige un ordenamiento para las letras DEF, es decir, se pueden tener P(3, 3) = 3! = 6 formas distintas de ordenar dischas letras, el segundo paso puede realizarse de de P(4, 4) = 4! = 24, ya que se considera cualquiera de las ordenaciones del primer paso como un elemento, más A, B y C. Y por la regla del producto la respuesta es 6 · 24 = 144, permutaciones de dichas letras.

g) Supomgamos que una caja puede contener tantas peloltas como se quiera. Se quieren colocar 3 pelotas de colores diferentes en 10 cajas con numeracón distinta. La primer pelota puede colocarse en cualquiera de las 10 cajas, como puede hacerse con la segunda y tercera pelotas, por lo que el número total de colocaciones diferentes es 10 · 10 · 10 = 1,000 maneras diferentes de acomodar las pelotas.

En genral, hay n^r maneras de colocar r pelotas de colores dentro de n cajas numeradas, si una caja puede contener tantas pelotas como queramos.

Ahora regresemos con las combinaciones.

En problemas de conteo donde el orden es importante, las permutaciones-r son claramente relevantes. Muchas veces el orden no es importante, en cuyo caso la habilidad para contar conjuntos asquiere importancia. Sabemos que un conjunto S con n elementos tiene en total 2ⁿ subconjuntos. Para 0 r n sea el número de subconjuntos de S con r elementos. El número se llama coeficiente binomial y se lee "n en r" y en ocasiones se le llama el número de combinaciones de n objetos, tomando r a la vez.

Teorema:
Para 0 r n tenemos que

Demostración:
Sea S un conjunto con n elementos. Para cada subconjunto de T en S elementos, hay r! permutaciones de S que utilizan elementos de T. Por lo tanto hay permutaciones de S en total, es decir:

Ejemplos:
a) ¿Cuántas manos de poker hay en una baraja de 52 cartas?

Hay = 2'598,960 manos de poker.

b) Se quieren colocar 3 pelotas, todas ellas del mismo color, en 10 cajas que estas numeradas 1,2, ... , 10. Nuestro objetivo es conocer el número de maneras distintas en que las pelotas pueden distribuirse, si cada caja puede contener sñolo una pelota.

La respuesta es = 120 maneras distintas de colocar las pelotas.

c) Una ama de cada desea programar cenas de espagueti 3 veces a la semana. La cantidad de maneras distintas de programarlas es = 35.

d) Un grupo de 5 estudiantes: Mary, Boris, Rosa, Ahmad y Nora, han decidido hablar con el jefe del Departamento de Matemáticas para que el departamento ofrezca más cursos de Matemáticas Discretas. El jefe ha avisado que hablará solamente con 3 estudiantes en su oficina. ¿De cuántas maneras pueden elegir estos 5 estudiantes 3 de ellos para hlablar con el jefe del Departamento?.

La respuesta es = 10 maneras diferentes.

e) ¿De cuantas formas puede elegirse un comié de 3 personas de entre un grupo de 10 personas distintas?.

En total se tienen = 120 maneras distintas de elegirlas.

f) ¿De cuántas maneras distintas puede elegirse un conité de dos mujeres y 3 hombres de un grupo de cinco mujeres distintas y seis hombres distintos?.

Las mujeres pueden elegirse de = 10 formas y los hombre pueden elegirse de = 20 formas. Y por la regla del producto tenemos que el número total de comités es 10 · 20 = 200.

g) ¿Cuántas cadenas de 8 bits contiene exactamente 4 unos?

La respuesta es = 70 formas o cadenas diferentes.