Para ver estos recursos será más fácil si empezamos con un
Ejemplo:
En el menú de un restaurante se tienen dos
entradas, tres platos principales y cuatro bebidas ¿Cuántas posibles
combinaciones de comidas diferentes constan de un plato principal y una bebida?
Primeramente veamos el menú:
|
Entrada
|
Plato Principal
|
Bebidas
|
| Nachos (N) | Hamburguesa (H) | Te (T) |
| Ensalada (E) | Hamburguesa con queso (Q) | Leche (L) |
| Filete de Pescado (F) | Café (C) | |
| Cerveza de Raíz (R) |
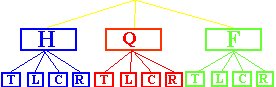
Si listamos todas las posibles comidas que constan de un plato principal y una bebida
HT, HL, HC, HR, QT, QL, QC, QR, FT, FL, FC, FR
se ve que hay 12 comidas diferentes. Ya que hay 3 platos principales y 4 bebidas, por la regla del producto 3 · 4 = 12 comidas diferentes.
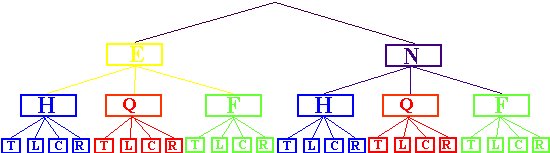
Además existen 24 comidas diferentes que constan de una entrada, un plato principal y una bebida, las cuales son:
NHT, NHL, NHC, NHR, NQT, NQL, NQC, NQR, NFT, NFL, NFC,
NFR
EHT, EHL, EHC, EHR, EQT, EQL, EQC, EQR, EFT, EFL, EFC, EFR
Y se observa que como hay dos entradas, tres platos principales y cuatro bebidas, se tiene, que por la regla del producto, existen 2· 3 · 4 = 24 comidas diferentes.
Se pueden representar las posibles comidas no solamente por listas que sirven para enumarar las posibles opciones, también se pueden representar mediante árbolers, como se muestra a continuación.

En la figura anterior se representan las 12 posibles opciones de elegir una comida que conste de un plato principal y de una bebida.
En cambio el siguiente árbol muestra las 24 diferentes opciones que constan de una entrada, un plato principal y una bebida.