4.1 REGLAS DE LA SUMA Y EL PRODUCTO
Definición:|![]() |=0
y |{1,2,3...n} | = n
|=0
y |{1,2,3...n} | = n ![]() n
n![]()
![]() +
+
a) Si ![]() y
y ![]() son disjuntos,
es decir,
son disjuntos,
es decir, ![]()
![]()
![]() =
= ![]() , entonces
|
, entonces
|![]()
![]()
![]() |
= |
|
= |![]() | + |
| + |![]() |
|
b) En general |![]()
![]()
![]() |
= |
|
= |![]() | + |
| + |![]() |
|
![]() |
|![]()
![]()
![]() |
|
La razón intuitiva por la que se cumple b) es que cundo
calculamos |![]() | +
|
| +
|![]() | se estan contando
dos veces los elementos de
| se estan contando
dos veces los elementos de ![]()
![]()
![]() ,
por lo que debemos restar |
,
por lo que debemos restar |![]()
![]()
![]() |
de la suma de |
|
de la suma de |![]() |
+ |
|
+ |![]() | para obtener
|
| para obtener
|![]()
![]()
![]() |.
|.
Sea C el conjunto de los alumnos que toman la clase de computación y sea F el conjunto de los alumnos que toman la clase de física. Aplicando la regla de la suma tenemos que:
| |C |
= |C| + |F| |
| = 20 + 30 - 7 | |
| = 43 |
Es decir, en total hay 43 alumnos.
b) ¿Cuántos enteros en S = {1, 2, 3, ..., 1000} son divisibles por 3 o 5?
Sean:
D3 = {n ![]() S | n es divisible por 3}
S | n es divisible por 3}
D5 = {n ![]() S | n es divisible por 5}
S | n es divisible por 5}
Buscamos el número de elementos en D3 ![]() D5, que no es obvio. Puede verse que | D3 | =333; basta dividir 1000 entre 3
y redondear.De la misma manera | D5 | = 200. Además |D3
D5, que no es obvio. Puede verse que | D3 | =333; basta dividir 1000 entre 3
y redondear.De la misma manera | D5 | = 200. Además |D3 ![]() D5| = |D15| = 66.
D5| = |D15| = 66.
Por b) de la Regla de la Suma tenemos que:
| D3 ![]() D5 | = 333 + 200 – 66 = 467 números enteros que son divisibles por
3 o 5.
D5 | = 333 + 200 – 66 = 467 números enteros que son divisibles por
3 o 5.
c) La biblioteca de una universidad tiene 40 libros de texto de sociología y 50 de antropología. Por a) de la Regla de la Suma, un estudiante de esta universidad puede elegir entre 40 + 50 libros de texto para aprender acerca de alguno de estos temas.
d) Un instructor de ciencias de la computación tiene cinco
libros de cada uno de los siguientes lenguajes de programación: Basic,
Fortran, C, Pascal, por lo que puede recomendar cualquiera de estos veinte libros
a un estudiante interesado en aprender un lenguaje de programación.
Ahora, el ejemplo anterior muestra que se puede generalizar esta regla.
Así
| |A |
|= | (A |
| = |(A |
|
| = | A | + | B | - | A |
|
| = | A | + | B | - | A |
|
| = | A | + | B | + | C | - | A |
y en general:
Si A1, …, An son n conjuntos finitos con cardinalidades | A1| , . . . , | An|, se verifica que:
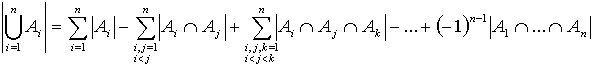
Ahora bien, si A = { A1, A2, . . . , An} son una partición del conjunto A, entonces el principio se reduce a:
| A | = | A1| + | A2|
+ . . . + | An |, o bien | A1
![]() A2
A2
![]() . . .
. . . ![]() An | = | A1| + | A2|
+ . . . + | An |
An | = | A1| + | A2|
+ . . . + | An |
Regla del Producto (Principio de Elección)
| S ![]() T | = | S | · | T | = 2 · 3 = 6, dichos elementos
son:
T | = | S | · | T | = 2 · 3 = 6, dichos elementos
son:
S ![]() T = {( 1, a ), (1, b), (1, c), (2, a), (2, b), (2, c)}
T = {( 1, a ), (1, b), (1, c), (2, a), (2, b), (2, c)}
Regla del Producto
a) Para conjuntos finitos S1, S2,
. . Sk se tiene que:
![]()
b) De manera más general, supongamos que un conjunto dado puede verse como k-adas ordenadas (s1,...,sk) con la siguiente estructura: Hay n1 elecciones posibles S1. Dado S1 hay n2 elecciones posibles S2. Dados S1 y S2 hay n3 elecciones posibles de S3. En general dados S1,.... Sj-1, hay nj elecciones posibles Sj. Entonces el conjunto tiene n1 · n2 · . . . · nk elemento.
Ejemplos:b) Calculemos ahora la forma de seleccionar 5 cartas distintas sin reemplazo de una baraja de 52 cartas. Sin reemplazo significa que una vez seleccionada una carta ya no es posible regresarla a la baraja. Esta vez a) de la regla del producto no puede aplicarse, ya que están prohibidas las quintillas donde se repita una carta. Sin embargo podemos aplicar la regla b) del producto. La primera carta puede seleccionarse de 52 maneras. Una vez seleccionada, la segunda carta puede elegirse de 51 maneras. La tercera puede escogerse de 50 formas, la cuarta de 49 y la quinta de 48. De manera que para elegir 5 cartas sin reemplazo existen 52 · 51 · 50 · 49 · 48 formas diferentes.
c) El club de teatro de la Universidad realiza ensayos para una obra de teatro que se montará el próxima año. Si seis hombres y ocho mujeres ensayan para los papeles principales (masculino y femenino), por la regla del producto, el director puede elegir a la pareja principal de 6 · 8 = 48 formas diferentes.
d) En una fabrica de placas de automóvil, cada placa consta de dos letras y cuatro dígitos:
i) Si ninguna letra o dígitos se pude repetir habrá:
27 · 26 · 10 · 9 · 8 · 7 = 3'538,080 placas
posibles diferentes.
ii) Si se permite repetir las letras y los dígitos
será posible tener
27 · 27 · 10 · 10 · 10 · 10 = 7'290, 000
placas diferentes.
iii) Si no permite que dos dígitos juntos se repitan,
entonces habrá:
27 · 27 · 10 · 9 · 9 · 9 = 5'314,410 placas
diferentes.