Ahora se deben de combinar la solución homogénea y la solución particular y determinar los coeficientes indeterminados de la solución homogénea. Para una relación de recurrencia de k-ésimo orden, los k coeficientes indeterminados

A₁, A₂, A₃, ..., A_k

de la solución homogénea puden determinarse mediante los valores iniciales:

para cualquier r_o

Si todas las raíces de la ecuación de recurrencia son distintas, la solución total es de la forma

donde p(r) es la solución particular.

Así para , se tiene el siguiente sistema de ecuaciones lineales

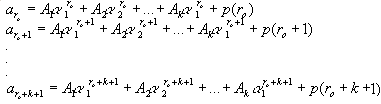
Estas k ecuaciones pueden resolverse para

A₁, A₂, A₃, ..., A_k

Ejemplo:
Sea la ecuación de recurrencia :

La solución homogénea es:

y la solución particular es

= 16 · 4^r

Y ahora supongamos que nos dan los valores iniciales (condiciones de frontera) a₂ = 278 y a₃ = 962

Entonces la solución total es

Sustituyendo los valores se tiene que

278 = 9A₁ + 4A₂ + 256

962 = -27A₁ - 8A₂ + 1024

Donde se obtiene que

A₁ = 2 y A₂ = 1

Así

a_r = 2(-3)^r + (-2)^r +16·4^r