Definición:
Intuitivamente una sucesión es una simple lista de objetos llamados elementos, que forman un conjunto, los elementos están uno detrás de otro en el orden natural creciente de los números naturales .

Si la sucesión es finita, puede terminar después de un cierto numero de términos o puede en principio, al menos, seguir indefinidamente, en este caso se dice que es infinita.

Ejemplo:
La sucesión 1, 4, 9, 16, 25, ... , n², es una sucesión infinita de números n al cuadrado, los tres puntos suspensivos significan "así sucesivamente".

Una sucesión general, es decir, una sucesión en la que no se especifican los términos puede escribirse como:

x₁, x₂, x₃, …

o algunas veces como:

x_n, 1 n

Si X es una sucesión se escribe como X = (x_n).

Formalizando, una sucesión es una función de una variable n donde Dom(n) = , a cada n le corresponde un termino de la sucesión (x_n), el termino n-ésimo de la sucesión, es decir:

: (x_n)

En una sucesión los términos pueden ser todos distintos o no ,esto es puede tener términos repetidos.Por ejemplo = {1,0,0,1,1,0,1,0,1} es una sucesión finita con términos repetidos.

Ejemplos de sucesiones:
1, 2, 3, 4, ..., n, ...
2, 4, 6, 8, ..., 2n, ...
1, 4, 9, 16, ..., n², ...
-1, 1, -1, 1, ..., -1ⁿ, ...
-1, 2, -3, 4, ..., (-1)ⁿn, ...
-1, 1/2, -1/3, 1/4, ..., -1ⁿ/n, ...
1/2, 1/4, 1/8, 1/16, ..., 1/2ⁿ, ...
1/10, 1/100, 1/1000, 1/10000, ..., 1/10ⁿ, ...

Progresiones Aritméticas

Empecemos viendo un ejemplo:

Escalera de Jacob.
En el rasca cielos que Jacob posee hay una escalera que va desde el suelo hasta la cima .El primer escalón mide 8 pulgadas y los posteriores miden 9 pulgadas. ¿A que altura del suelo esta el escalón 800?

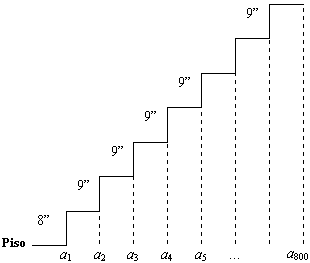
a₁ = 8
a₂ = 8 + 1(9) = 17
a₃ = 8 + 2(9) = 26
a₄ = 8 + 3(9) = 35
.
.
.
a₈₀₀ = 8 + 799(9) = 7199

Por lo tanto el escalón 800 esta a 7199 pulgadas sobre el suelo.

Ahora consideremos las siguientes sucesiones. Al detectar un patrón llénese los espacios en blanco.

a) 5, 9, 13, 17, , , ...

b) 2, 2.5, 3, 3.5, , , ...

c) 8, 5, 2, -1, , , ...

¿Qué tienen en común estas tres sucesiones? Simplemente que en cada caso se puede obtener un término sumando un número fijo al anterior.

Definición:
Una progresión aritmética es una sucesión infinita de números donde cualquier termino (distinto de primero) se obtiene sumando un numero fijo al anterior.

Si se denota a tal sucesión como a₁, a₂, a₃, ... satisface la formula recursiva

a_n = a_n-1 + d

donde d es un numero fijo llamado diferencia común.

¿Se puede obtener también una fórmula explícita= Si. Veamos primero la siguiente figura:

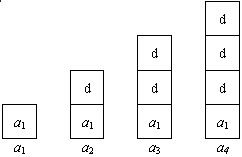
Hay que observar que las d's deben sumarse con a₁ una vez menos que el subíndice de a. Esto significa que:

a_n = a₁ + (n - 1)d

Entonces:
a_n = 5 + (n - 1)(4) = 1 + 4n

b_n = 2 + (n - 1)(.5) = 1.5 + .5n

c_n = 8 + (n - 1)(-3) = 11 - 3n

Progresiones Geométricas

Empecemos viendo un ejemplo:

Escalera de Oro de Jacob.
En sus sueños Jacob vio una escalera de oro con ángeles subiendo y bajando. El primer escalón era de 8 pulgadas, pero después cada escalón tenia una altura de 5/4 pulgadas mas que el anterior. ¿A que altura estará el escalón 800?

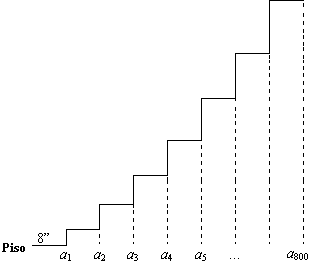
a₁ = 8
a₂ = 8 (5/4)
a₃ = 8 (5/4)²
a₄ = 8 (5/4)³
.
.
.
a₈₀₀ = 8 (5/4)⁷⁹⁹

Por lo tanto la altura del escalón 800 es de 8 (5/4)⁷⁹⁹ pulgadas arriba del piso.

Esta escalera de Jacob es en verdad para ángeles y no para personas.
El escalon 800 tiene 3.4 x (10)⁷³ millas de alto. A modo de comparación, el sol esta a 9.3 x (10)⁷ millas de la tierra y Alpha Centauri, que es la estrella más cercana a la tierra, esta a 2.5 x (10)¹³ millas de la misma. Esta escalera en verdad alcanza el cielo.

En la sucesión anterior cada término era 5/4 veces más alto que el anterior. Se puede encontrar un patrón similar en cada una de las siguientes sucesiones:

a) 3, 6, 12, 24, , , ...

b) 12, 4, 4/3, 4/9, , , ...

c) .6, 6, 60, 600, , , ...

El rasgo común de estas tres sucesiones es que en cada caso se puede obtener un término multiplicando el término anterior por un número fijo.

Definición:
Una progresión geométrica es una sucesión infinita de números donde cualquier término (distinto del primero), se obtiene multiplicando un numero fijo al termino anterior.

Asi una sucesión geométrica a₁, a₂, a₃, ... satisface la formula recursiva

a_n = r a_n-1

donde r es un número fijo llamado razón común.

Además se tiene a₂ / a₁ = a₃ / a₂ = a₄ / a₃= ... = a_n / a_n-1 = r.

Para obtener la formula explícita correspondiente se tiene que

a₂ = r(a₁)

a₃ = r(a₂) = r(r · a₁) = r²(a₁)

a₄ = r(a₃) = r(r² · a₁) = r³(a₁)
.
.
.
a_n = r^{n-1 ·} a₁

En este caso el exponente de r es uno menos que el subíndice de a. Esto significa que:

a_n = a₁ · r^n-1

Así:
a_n = (3)(2)^n-1

b_n = (12)(1/3)^n-1

c_n = (0.6)(10)^n-1