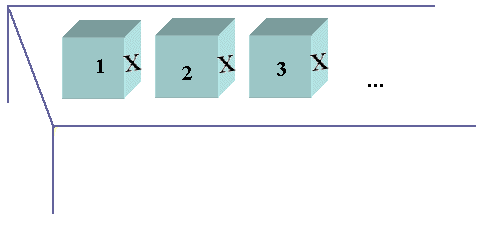
Supongamos que una serie de cubos numerados 1, 2, 3 están en una mesa infinitamente larga y que los cubos están marcados con una "X", como se muestra a continuación:

y supóngase que:
a) El primer cubo esta marcado.
b) Si todos los cubos anteriores al cubo (n + 1) están marcados, entonces el cubo (n + 1) también lo esta.
a) y b) implican que cada cubo esta marcado, examinando los cubos uno por uno.
La afirmación a) establece de manera explícita que el cubo 1 esta macado. Considerando el cubo 2, todos los cubos anteriores al cubo 2 estan marcados, o sea, el cubo 1 y así de acuerdo a b) el cubo 2 también está marcado. Considerando el cubo 3, todos todos los cubos anteriores al cubo 3 están marcados, o sea, los cuales 1 y 2 así de acuerdo a b) el cubo 3 esta marcado.
Para mostrar que el cubo 5 está marcado, se observa que todos los cubos anteriores al cubo 5 están marcados, de modo que por b), el cubo 5 también esta marcado.
Este ejemplo ilustra el principio de inducción matemática.
Para mostrar como se puede utilizar las inducción de manera más
profunda, sea ![]() n
la suma de los n enteros positivos
n
la suma de los n enteros positivos ![]() n
= 1 + 2+ +3 + ... + n
n
= 1 + 2+ +3 + ... + n
Ahora supongamos que alguien afirma que:
para n = 1, 2, 3, ...
Esto establece una serie de afirmaciones:
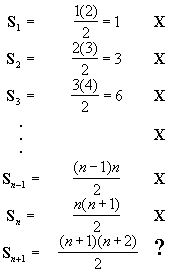
Supongamos que cada ecuación verdadera tiene una X junto a ella. Como la primera ecuación es verdadera, ésta marcada.
Ahora debemos demostrar que si todas las ecuaciones anteriores a la ecuación (n +1) son verdaderas, entonces la ecuación (n + 1) también lo es.
Suponiendo que todas las ecuaciones anteriores a la ecuación (n +1) son verdaderas, entonces la ecuación (n) es verdadera:
Debemos demostrar que la ecuación (n +1)
![]()
es verdadera. De acuerdo a la definción:
| 1 + 2 + 3 + ... + n + (n + 1) |
![]() n
esta contenida dentro de
n
esta contenida dentro de ![]() n+1
en el sentido de que
n+1
en el sentido de que
|
|
= |
1 + 2 + 3 + ... + n + (n + 1) |
|
= |
De donde se obtiene que:
|
= |
+ 2 + 3 + ... + n + (n + 1) |
||
|
= |
+ (n +1) | ||
|
= |
|||
Otro ejemplo seria ![]() n
= 1 + 3 + 5 + ... + (2n -1) = n², para
n = 1, 2, 3, ...
n
= 1 + 3 + 5 + ... + (2n -1) = n², para
n = 1, 2, 3, ...
Es decir, la suma de los n primeros números impares es n². Donde tenemos que
| = 1² = 1 | |
| = 2² = 4 | |
| = 3² = 9 | |
| . . . |
|
| = (n - 1)² | |
| = n² |
Donde se observa que ![]() 1
es verdadera.
1
es verdadera.
Suponiendo que ![]() n
es verdadera, debemos demostrar que la ecuación (n + 1),
n
es verdadera, debemos demostrar que la ecuación (n + 1), ![]() n+1
= (n +1)², es verdadera. El n-ésimo término
es (2n - 1), entonces el siguiente seria (2n + 1).
n+1
= (n +1)², es verdadera. El n-ésimo término
es (2n - 1), entonces el siguiente seria (2n + 1).
De acuerdo a la definición:
| = 1 + 3 + 5 + ... + (2n -1) + (2n + 1) | |
| = |
|
| = n² + (2n + 1) | |
| = n² + 2n + 1 | |
| = (n + 1)² |