Definición:
El tamaño de un conjunto es la cantidad de elementos distintos del conjunto.

Ejemplos:
a) El tamaño del conjunto {a, b, c} es 3

b) El tamaño del conjunto {a, o, d} es 3

c) El tamaño del conjunto {{a, b}} es 1

d) El tamaño del conjunto es cero

Para encontrar el tamaño de dos conjuntos de manera comparativa, se necesita la siguiente

Definición:
Dados dos conjuntos P y Q se dice que existe una correspondencia uno a uno (Biunicova) entre los elementos de P y los de Q, si es posible “aparear” los elementos de P y de Q de tal modo que todos los elementos P estén aparecidos con distintos elementos de Q.

Ejemplo:
Existe una correspondencia biunívoca entre los elementos de {a, b} y los de {c, d}, también existe una correspondencia biunívoca entre los de {a, b, c} y los de {0, a, b}, pero no existe una correspondencia biunívoca entre los elementos de {a, b, c} y los de {a, d}.

Definición:
Se dice que un conjunto es finito si existe una correspondencia biunívoca entre los elementos del conjunto y los elementos de algún conjunto n , y se dice que n es la cardinalidad del conjunto.

Ejemplo:
La cardinalidad de los conjuntos {a, b, c}, {a, o, d}, {1, 2, 3}, {,{},{, {}}} es 3

Definición:
Se dice que un conjunto es infinito contable (o inifito numerable o que la cardinalidad del conjunto es infinita contable), si existe una correspondencia uno a uno entre los elementos del conjunto y los elemento de .

Ejemplos:
El conjunto de los números naturales ={1, 2, 3, ... } es un conjunto infinito contable.

El conjunto de todos los enteros pares no negativos { 2, 4, 6, ...}es un conjunto infinito contable, pues existe una correspondencia uno a uno entre los enteros pares no negativos y los números naturales, a saber el entero 2i le corresponde el número natural i, para i = 1, 2, ..., es decir:

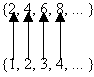
De manera análoga, el conjunto de todos múltiplos de 7 no negativos {7, 14, 21, ... }es infinitos numerable, es decir:

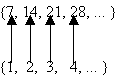
Cabe señalar que un conjunto es infinito contable si, comenzando con un cierto elemento podemos listar sucesivamente, uno detrás de otro todos los elementos del conjunto, pues esa lista nos permite construir una correspondencia uno a uno entre los elementos del conjunto y los números naturales .

Ejemplo:
El conjunto de los enteros = { ..., -3, -2, -1, 0, 1, 2, 3, ... }, es un conjunto infinito contable, porque sus elementos pueden ser listados como = { 0, 1, -1, 2, -2, 3, -3, ...}, ya que se puede hacer una correspondencia uno a uno entre los elementos del conjunto de los enteros y los números naturales , es decir:

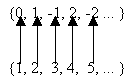
La unión de un número finito contable de conjuntos infinitamente contable es un conjunto infinito contable. Lo mismo sucede con la unión de un número infinito contable de conjuntos infinitos contables.

Ejemplo:
El conjunto de los números racionales es un conjunto infinito numerable ya que puede ser listado como sigue:

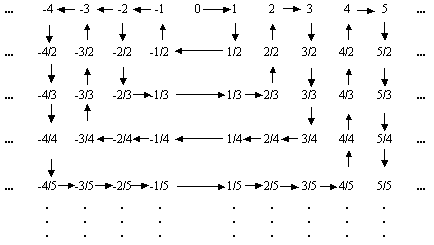
Además se puede observar que se pueden hacer una cantidad infinita numerable de sublistas, donde cada una es a la vez un conjunto infinito numerable, y la unión de todas ellas es el conjunto de los números racionales .