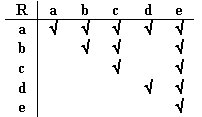Definición:
Se dice que una relación sobre un conjunto A es una relación de orden parcial si esta es reflexiva, antisimétrica o transitiva.

Si es un orden parcial sobre A, se utiliza la notación a b para indicar que (a, b) . Esta notación sugiere que estamos interpretando la relación como orden sobre los elementos.

Ejemplo:
Sea A={a, b, c, d, e} y sea una relación sobre A definida como sigue:

= {(a, a), (a, b), (a, c), (a, d), (a, e), (b, b), (b, c), (b, e), (c, c), (c, e), (d, d), (d, e), (e, e)}

Representada en la siguiente tabla:

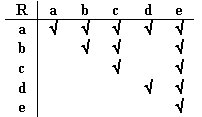
como es reflexiva, antisimétrica y transitiva por lo tanto es una relación de orden parcial.

Un conjunto A junto con un orden parcial sobre A, es llamado un conjunto parcialmente ordenado y se depota por (A, ). Un conjunto parcialmente ordenado es conocido como POSET (del inglés: partially ordered set).

Ejemplo:
Sea A el conjunto de y sea una relación sobre A , tal que (a, b) si a divide a b (con residuo igual a cero).

Entonces como cualquier entero se divide a si mismo, es una relación reflexiva. Si a divide a b significa que b no divide a a, a menos que sea a = b, por lo que es antisimétrica, y puesto que si a divide a b y b divide a c entonces a divide a c, por lo que es transisitva. enconsecuencia es un orden parcial.

En realidad un conjunto parcialmente ordenado es denotado como (A, ).

Definición:
Si es un orden parcial sobre A y si x, y A y x y y x, se dice que x y y son comparables . Y si x, y A y x y y x, se dice que x y y son incomparables.

Definición:
Una relación sobre un conjunto A que es irreflexiva, simétrica y transitiva es llamada de orden propia y se denota <.

Definición:
Si cada par de elementos de A son comparables se dice que es un orden total, es decir, un orden parcial es un orden total, (orden lineal ) si y solo si x,y, x y ó y x es siempre verdadero.

En este caso (A, ) es un conjunto totalmente ordenado ó también llamado cadena (chain).

Ejemplo:
Los números naturales con la relación (, ) y los números enteros con la relación (, ) son ambos cadenas.

También el conjunto de las palabras del idioma español con el orden lexicográfico es una cadena.

Definición:
La longitud de una cadena es la cantidad de elementos de la misma .

Definición:
Si todos los elementos de un conjunto A son no comparables, entonces se dice que es una anticadenas, es decir, un orden parcial es una anticadena si x, y A, x y y x.

En este caso (A, ) es una anticadena.

Ejemplo:
Sean A = {a, b, f, d, e} y sea un orden parcial. Entonces (A, ) es un conjunto parcialmente ordenado donde:

{a, b, c, e} cadena
{a, b, c} cadena
{a, d, e} cadena
{a} cadena
{b, d} anticadena
{c, d} anticadena

Representemos a por medio de una tabla.