Definición:
Una partición de un conjunto 
es
una colección de subconjuntos disjuntos no vacios de
que tienen a como
su unión, en otras palabras, la colección de subconjuntos Ai,
i 
I (donde
I es un índice del conjunto) forma una partición si y solo si:
cuando i 
j
y 
También se suele decir que estos subconjuntos son llamados
bloques de la partición ={A1,
A2, ... , Ak}
Ejemplo:
Sea ={a,
b, c, d, … , z} y sean
W1 = {a, e, i, o, u}
W2 = {w, c}
W3 = {b, f, g, h, j, k, l}
W4 = {m, n, ñ, p, q}
W5 = {r, s, t, v}
W6 = {x, y}
W7 = {d, z}
= W1 
W2
W3 W4
W5 W6
W7 o bien
={{a,
e, i, o, u}, {w, c}, {b, f, g, h, j, k, l}, {m, n, ñ, p, q}, {r, s, t,
v}, {x, y}, {d, z}}
Ejemplo:
Si ={a,b,c,d,e,f,g}
entonces {{a},{b,c,d},{e,f},{g}} es una partición de
y también se puede representar como 
,
en dondese coloca una barra sobre los elementos del mismo bloque.
TEOREMA 1:
Sea S una partición sobre un conjunto X. Decimos
que x 
y si para
algún A en
x, y
A. Entonces es reflexiva,
simétrica y transitiva.
Ejemplo:
Sea X = {1, 2, 3, 4, 5, 6} y sea ={{1,
3, 5},{2, 6},{4}} una partición de X. La relación
definida por el teorema anterior es:
={(1
,1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5), (2, 2),
(2, 6), (6, 2), (6, 6), (4, 4)}
Definición:
Una relación
que es reflexiva, simétrica y transitiva, sobre un conjunto X, se conoce
como una relación de equivalencia sobre X.
Ejemplos:
Sea X = {1, 2, 3, 4, 5, 6} y sea ={{1,
3, 5},{2, 6},{4}} una partición de X. La relación
definida por el teorema 1 es:
={(1
,1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5), (2, 2),
(2, 6), (6, 2), (6, 6), (4, 4)}
la cual, por la defición anterior es una relación de equivalencia. Si se representa por medio de digrafos tenemos que:
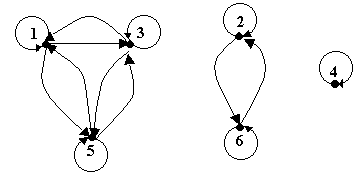
es
reflexiva puesto que (1, 1), (2, 2), (3, 3), (4, 4), (5, 5)
es simétrica
ya que siempre que si (x, y)
también (y,
x)
es transistiva puesto
que siempre que si si (x, y) y (y, z)
también (x,
z)
y como
es relfexiva, simétrica y transitiva, entonces
es una relación de equivalencia sobre X.
Ahora sea
= {(1, 1), (1, 2), (1, 3), (1, 4) , (2, 2), (2, 3), (2, 4) , (3, 3), (3, 4),
(4, 4)}, y sea X= {1, 2, 3, 4}
.es
reflexiva ya que (1, 1), (2, 2), (3, 3), (4, 4)
no es simetrica
ya que (2, 1), (3, 1), (4, 1), (3, 2), (4, 3), (4, 2) 
es transistiva puesto
que siempre que si si (x, y) y (y, z)
también (x,
z)
por lo que como
no es simétrica, por lo tanto no es una relación de equivalencia.
Definición:
Sea
una relación de equivalencia sobre un conjunto A. El conjunto de todos
los elementos que están relacionados a un conjunto de A es llamado clase
de equivalencia de A y se denota por [a], en otras palabras:
[a] = {x
A | x
a}
además se tiene
={[a] | a
A} es una partición de A
Ejemplos:
Sea A={1,2,3,4,5,6} y sea
= {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5),(5, 1), (5, 3), (5, 5), (2,
2), (2, 6), (6, 2), (6, 6), (4, 4)} una relación de equivalencia sobre
A, entonces tenemos que:
[1] = {1, 3, 5}, [2] = {2, 6}, [3] = {1, 3, 5}, [4] = {4}, [5] = {1, 3, 5} y [6] = {2 ,6}; donde se observa que
[1] = [3] = [5] = {1,3,5}, [2] = [6] = {2, 6}y [4]={4},
Ademas
= {{1, 3, 5}, {2, 6}, {4}} es una partición de A
Sea A={1, 2, 3, 4} y sea ={(1,
1), (1, 2), (2, 1), (2, 2), (3,3), (3, 4), (4, 3), (4, 4)}una relación
de equivalencia sobre A, donde se tiene que
[1] = {1, 2}, [2] = {1, 2}, [3] = {3, 4} y [4]={3, 4}, por lo que
[1] = [2] = {1, 2} y [3] = [4] = {3, 4}
donde
={{1,2},{3,4}} es una partición de A.
De los ejemplos anteriores se concluye que:
a) Si a
b entonces [a] = [b]
b) Si [a] = [b] entonces [a] 
[b] 
c) Si [a]
[b]
entonces a
b
En resumen dos clases de equivalencia de dos elementos de A son identicas o disjuntas.