Definición:
Una relación sobre un conjunto A es llamada reflexiva si (a, a) a A, es decir:

es reflexiva   a (a a)

Primeramente definamos algunas relaciones que nos serán utiles a lo largo de este tema.
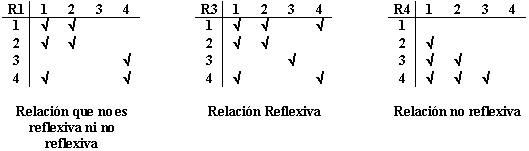
Sea A = {1, 2, 3, 4} y sean

R1 = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 1), (4, 4)}
R2 = {(1, 1), (1, 2), (2, 1)}
R3 = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)}
R4 = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}
R5 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}
R6 = {(3, 4)}

Ejemplo:
¿Cuáles relaciones son reflexivas? R3 y R5

Definición:
Una relación R sobre un conjunto A es llamada no reflexiva (o irreflexiva) si el par ordenado (a, a) , a A, es decir:

es no reflexiva   a (a a)

Ejemplo:
¿Cúales de las relaciones descritas no son reflexivas? R4 y R6

Mientras que R1 y R2 no relaciones que no son ni reflexiva ni no reflexivas.

Por medio de tablas podemos mostrar este tipo de relaciones.

Definición:
Una relación en un conjunto A es llamada simétrica si (a, b) implica que (b, a) , es decir:

es simétrica  a b (a b b a)

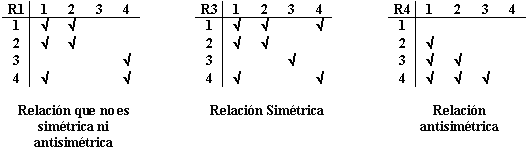
¿Cuáles de las anteriores relaciones representan una relación simétrica? R2 y R3

Definición:
Una relación en un conjunto A es llamada antisimétrica si (a, b) y (b, a) , entonce a = b, a, b A, es decir:

es antisimétrica  a b (a b b a a = b)

Otra forma de expresarlo es diciendo que cuando a b se tiene que, a b ó b a.

¿Cuáles de la anteriores relaciones son antisimetrica? R4, R5 y R6, ya que no hay pares de elementos a y b con a b tales que (a, b) y (b, a) .

Por medio de tablas podemos mostrar este tipo de relaciones.

Defición:
Una relación en un conjunto A es llamada transitiva si a, b, c A, (a, b) y (b, c) entonces (a, c) , esto es:

es transitiva  a b c (a b b c a c)

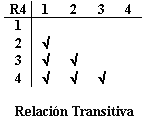
¿Cuáles de las anteriores relaciones representan una relación transitiva? R4 y R5.

Por medio de una trabla seria:

Ya que se tiene que:
(3, 2) y (2, 1) (3, 1)
(4, 2) y (2, 1) (4, 1)
(4, 3) y (3, 1) (4, 1)
(4, 3) y (3, 2) (4, 2)

Un grafo dirigifo de una relación transitiva tiene la propiedad que si existen aristas dirigidas de x a y y de y a z, también existe una arista dirigida de x a z. Como lo muestra el siguiente grafo

Sea una relación Binaria sobre A. La extensión transitiva de , denotada por , es una relación Binaria sobre A tal que contiene a y además si (a, b) y (b, c) entonces (a, c)

Ejemplo:
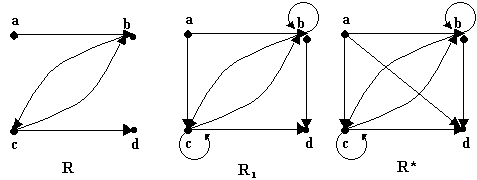
Sean A = {a, b, c, d} y = {(a, b), (b, c), (c, b), (c, d)}, entonces

= {(a, b), (a, c), (b, b), (b, c), (b, d), (c, b), (c, c), (c, d)}

Si es una Relación transitiva entonces es igual a

Si denota la extensión transitiva de , y en general denota la extensión transitiva de _i, definimos la cerradura transitiva de , denotada por , como el conjunto unión de , , , ... , entonces

= {(a, b), (a, c), (a, d), (b, b), (b, c), (b, d), (c, b), ( c, c), (c, d)}

Lo que por medio de digrafos se puede representar como: