Sea una relación de A en B y una relación de B en C. La composición de y es una relación consistente de los pares ordenados (a, c), donde a A y c C y para los cuales existe un b B tal que (a, b) y (b, c) , es decir a b y b c.

La composicón se denota por , si y son relaciones.

Ejemplos:
a) Sea A={1, 2, 3}, B={1, 2, 3, 4} y C={0, 1, 2} y sean

={(1, 1), (1, 4), (2, 3), (3, 1), (3, 4)}

={(1 ,0),(2, 0), (3, 1), (3, 2), (4, 1)}

Entonces ={(1, 0), (3, 0), (1, 1), (3, 1), (2, 1), (2, 2)}

b) Sean A={1, 2, 3}, B={2, 4, 6, 8} C={s, t, u} y sean

={(1, 2), (1, 6), (2, 4), (3, 4), (3, 6), (3, 8)}

={(2, u), (4, s), (4, t), (6, t), (8, u)}

Entonces ={(1, u), (1, t), (2, s), (2, t), (3, s), (3, t), (3, u)}

c) Sean A={a, b, c, d}, B={s, t, u, v} C={1, 2, 3, 4, 5} y sean

={(a, s), (a, t), (c, v), (d, u)}

={(s, 2), (t, 1), (t, 4), (u, 3)}

Entonces ={(a, 1), (a, 2), (a, 4), (d, 3)}

y graficamente se puede representar como

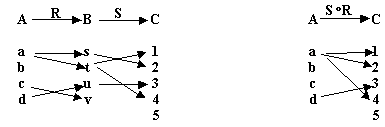
NOTA:

Generalizando:

Sean una relación de A en B, una relación de B en C y una relación de C en D.

La composición de , y es una relación consistente de los pares ordenados (a, d), donde a A y d D y para los cuales existen un b B y un c C tal que (a, b) , (b, c) y (c, d) , es decir a b, b c y c d.

Lo anterior se puede denotar como (), si , y son relaciones.

Además se tiene que () = ()