Puesto que las relaciones binarias son conjuntos de pares ordenados, las nociones de intersección, diferencia simétrica, unión y diferencia de dos relaciones, se obtienen de manera similar a las correspondientes para conjuntos.

Entonces primeramente es necesario recordar dichas nociones para conjuntos.

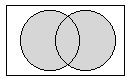
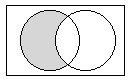
a) La unión de dos conjuntos A y B, denotada por AB, es el conjunto cuyos elementos son exactamente los elementos de A ó B, ó de ambos.

1) Si A = {a, b}, B = {c, d}, entonces AB = {a, b,c, d}

2) Si A = {a, b}, B = {a, c}, entonces AB = {a, b, c}

3) Si A = {a,b}, B = {}, entonces AB = {a, b}

4) Si A = {a, b}, B = {c, {a, b}}, entonces AB = {a, b, c, {a, b}}

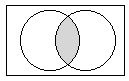
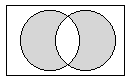
b) La intersección de dos conjuntos A y B, denotada por A B, es el conjunto cuyos elementos son exactamente los elementos que están tanto en A como en B.

1) {a, b} {a, c} = {a}

2) {a, b} {c, d} = {}

3) {a, b} {} = {}

c) La diferencia de dos conjuntos A y B, denotada por A B, es el conjunto que contiene exactamente aquellos elementos de A que no estan en B.

1) {a, b, c}{a} = {b, c}

2) {a, b, c}{a, d} = {b, c}

3) {a, b, c}{d, e} = {a, b, c}

d) La diferencia simetrica de dos conjuntos A y B, denotada por A B, es el conjunto que contiene todos los elementos que están en A o en B pero no en ambos, es decir, A B = (A B) (A B).

1) {a, b} {a, c}={b, c}

2) {a, b} {}= {a, b}

3) {a, b} {a, b}={}

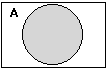
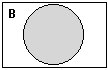
Graficamente se pueden representar estas operaciones con conjuntos como sigue:

	Conjunto A	Conjunto B
A B	A B	A B	A B

Aplicando los conceptos anteriores a relaciones binarias, tenemos que si y son dos relaciones binarias de A a B entonces: , , , son también relaciones binarias de A a B.

Sean y dos relaciones de X a Y y de U a V respectivamente. Además tenemos que

Dom()={a, b, c} y Cod()={A, B, C}

Dom()={a,b} y Cod()={B,C}

Encontrar , , , , si ={(a, A), (a, B), (b, C)} y ={(a, B), (b, C)}

={(a, A), (a, B), (b, C)}

={(a, B), (b, C)}

={(a, A)}

={(a, A)}

Definición:
Puede definirse el complemento de una relación como el como el conjunto de todos los pares ordenados del producto cartesiano AB que no estan en , y se representa como ó ~.

Ejemplo:
Sean y dos relaciones de X a Y y de U a V respectivamente. Además tenemos que

Dom()={a, b, c} Cod()={A, B, C}, Dom()={a,b} Cod()={B,C} y sean

={(a, A), (a, B), (b, C)} y ={(a, B), (b, C)}

Entonces XY={(a, A), (a, B), (a, C), (b, A), (b, B), (b, C), (c, A), (c, B), (c, C)}

Por lo tanto ={(a, c), (b, A), (b, B), (c, A), (c, B), (c, C)}

Y para UV ={(a, B), (a, C), (b, B), (b, C)}

se tiene que ={(a, C), (b, B)}.

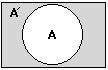
Otra operación que a menudo se utiliza es el inverso de una relación, la cual se define de la siguiente manera:

Definición:
Sea una relación de A a B, el inverso de , que de denota como ó , y es la relación de B a A definida formalmente como:

Ejemplo:
Sean A={2, 3, 4} y B={3, 4, 5, 6, 7}, además definimos como sigue:

(a, b) si a divide a b (división entera)

entonces = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}

por lo que = {(4, 2), (6, 2), (3, 3), (6, 3), (4, 4)}

De lo anterior se deduce que a b b a. Algunos autores llaman al inverso opuesto.

Como una relación es un conjunto, podemos obtener el número de elementos de dicho conjunto, es decir:

Definición:
La cardinalidad es el número de elementos de un conjunto para una relación de A en B. La cardinalidad se representa #.

Ejemplos:
Si A = {1,2,3,4}entonces #A = 4

Si = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}entonces # = 5

Definición:
Sea una relación de A en B el conjunto potencia , denotado como P(), es el conjunto que contiene a todos los subconjuntos de , es decir:

P() = {S | S A}

Si # = n, entonces #P() = 2ⁿ

Ejemplo:
Sea = {(1, 1), (1, 2), (1, 3)}, entonces # = 3 y #P() = 2^·3 = 8

P() = {, {(1, 1)}, {(1, 2)}, {(1, 3)}, {(1, 1), (1, 2)}, {(1, 1), (1, 3)}, {(1, 2), (1, 3)}, {(1, 1), (1, 2) ,(1, 3)}}