La forma más directa de expresar una relación entre elementos de dos conjuntos es usando pares ordenados, por lo que de manera abstracta sae puede definir una relación es como un conjunto de pares ordenados. En este contexto se considerará que el primer elemento del par ordenado está relacionado con el segundo elemento del par ordenado..

Definición:
Si A y B son dos conjuntos no vacios el producto cartesiano A B sera el conjunto de pares ordenados (a, b), donde a A y b B, es decir:

A B = {(a, b) | a A y b B}

Se usa la notación a b para denotar que (a, b) y a b para denotar que (a, b) .

Ejemplo:
Sean A = {1, 2, 3} y B = {r, s} entonces
A B = {(1, r), (1, s), (2, r), (2, s), (3, r), (3, s)}
B A = {(r, 1), (r, 2), (r, 3), (s, 1), (s, 2), (s, 3)}

Se puede ver que que AB es diferente de BA

Definición:
Una relación binaria, o simplemente relación, de un conjunto A en un conjunto B es un subconjunto del producto cartesiano A B. Si (a, b) se escribe a b y significa que a esta en relación con b.

Si A = B se dice que es una relación binaria sobre A.

Ejemplo:
Sea A = {1, 2, 3, 4} ¿Cuales pares ordenados están en la siguiente relación? = {(a, b) | a divide a b}

Nota: La división debe ser entera.

= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2),(2, 4), (3, 3), (4, 4)}, en ese caso es una relación binaria sobre A.

Definición:
Si (A B) es una relación de A en B, el dominio de , se escribe Dom(), y es el conjunto de los elementos de A que están relacionados con B, es decir:

Dom() = {a A | (a, b) , para algún b B}

Ejemplo:
Sean A = {1, 2, 3, 4} y B = {r, s} y sea = {(1, r), (1, s), (2, s), (3, s)}, entonces Dom() = {1, 2, 3}

Definición:
Si (A B) es una relación de A en B. El codominio (rango, imagen o recorrido) de , se escribe Cod() o Ran() y es el conjunto de los elementos de B, que están relacionados con algún elemento de A, es decir:

Cod() = {b B | (a, b) , para algún a A}

Ejemplo:
Sea A = {1, 2, 3, 4}  y   B = {r, s} además = {(1, r),(2, s),(3, r)} entonces Cod() = {r, s}

OTRAS REPRESENTACIONES DE LAS RELACIONES

Las relaciones además de ser representadas como conjuntos de pares ordenados, se pueden representar de las siguientes maneras:

a) Tablas
b) Diagramas
c)Matriz de Relación
d) Por medio de Grafos Dirigidos (digrafos).

Ejemplo:
Sean A = {1, 2, 3}  y B = {r, s} y sea = {(1, r), (1, s), (2, r), (3, s)}

a)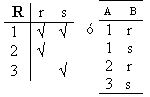

b)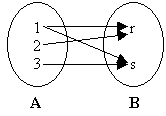

c)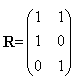

La representación por medio de grafos dirigidos, se utiliza cuando es relación binaria sobre A.

Ejemplo: Sea la relación sobre A = {1, 2, 3, 4}definida como sigue:

(x, y) si x y, si x, y A

Por lo que = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}

y su representación como digrafo es

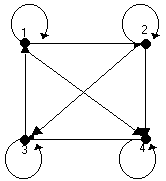
Este tipo de representaciones se analizará con más detalle en la unidad dedicada a grafos.
Los puntos son llamados vértices y representan los elementos de A.
Las flechas son llamadas aristas dirigidas de x a y y representan que el elemento (x, y) esta relacionado.
Las flechas que representan elementos de la forma (x, x) se llaman lazos.