NOMBRE DE LA MATERIA: MT102 ALGEBRA
DEPARTAMENTO DE ADSCRIPCION: DEPARTAMENTO DE MATEMATICAS
CARGA HORARIA SEMESTRAL: TEORIA: 60 PRACTICA: 0
CREDITOS:8 TIPO: CURSO
AREA DE FORMACION: BASICA COMUN
PREREQUISITOS: NINGUNO

OBJETIVO GENERAL: Adquirir la abstracción del álgebra, así como los principios de aplicación de los mismos y su integración a las ciencias exactas y la ingeniería. Desarrollar las demostraciones formales de los teoremas más importantes y establecer los conceptos de sistema y estructura matemática.
OBJETIVOS ESPECIFICOS: El alumno reforzará y aplicará los conceptos fundamentales del álgebra.
CONTENIDO TEMATICO:
1. EL CONJUNTO LOS NUMEROS REALES
1.1 Los números naturales y los números enteros
1.2 Los números racionales e irracionales
1.3 El campo de los números reales
1.4 Propiedades de los números
1.5 Relación de orden
1.6 Igualdades y desigualdades
1.7 Concepto de número imaginario
1.8 Concepto de número complejo

2. LAS CUATRO OPERACIONES FUNDAMENTALES
2.1 Definiciones
2.2 La relación de igualdad
2.3 Adición
2.4 Ley de los signos para adición
2.5 Adición de monomios y polinomios
2.6 Sustracción
2.7 Axiomas y teoremas de multiplicación
2.8 Leyes de exponentes en multiplicación
2.9 Multiplicación de dos o más monomios
2.10 El producto de dos polinomios
2.11 División
2.12 El cociente de dos polinomios

3. PRODUCTOS NOTABLES Y DESCOMPOSICION EN FACTORES
3.1 Algunos ejemplos sencillos por multiplicaci&ocute;n directa
3.2 Binomio de exponente entero y positivo
3.3 Binomio de exponente entero y negativo

4. FRACCIONES ALGEBRAICAS
4.1 Definiciones y principio fundamental
4.2 Conversión de fracciones
4.3 Multiplicación de fracciones
4.4 División de fracciones
4.5 El mínimo común denominador
4.6 Adición de fracciones
4.7 Fracciones complejas

5. ECUACIONES LINEALES Y FRACCIONARIAS
5.1 Definiciones
5.2 Ecuaciones equivalentes
5.3 Ecuaciones lineales de una incógnita
5.4 Ecuaciones fraccionarias

6. SISTEMAS DE ECUACIONES LINEALES SIMULTANEAS
6.1 Solución de un sistema como intersección de conjuntos
6.2 Métodos analíticos de solución
6.3 Sistemas de 2 y 3 ecuaciones
6.4 Solución de sistemas por medio de determinantes
6.5 Interpretación gráfica

7. ECUACIONES CUADRATICAS
7.1 Métodos de solución
7.2 Raíces reales
7.3 Raíces complejas
7.4 Factorización del trinomio cuadrático general
7.5 La suma y el producto de las raíces
7.6 Ecuaciones del tipo cuadrático
7.7 Ecuaciones con radicales
7.8 Algunos problemas geométricos

8. FRACCIONES PARCIALES
8.1 Resolución de fracciones
8.2 Factores lineales distintos
8.3 Factores lineales repetidos
8.4 Factores cuadráticos distintos
8.5 Factores cuadráticos repetidos

9. ECUACIONES ALGEBRAICAS DE GRADO SUPERIOR
9.1 Ecuaciones racionales
9.2 Teorema del residuo
9.3 Teorema del factor y su inverso
9.4 División sintética
9.5 Gráfica de un polinomio
9.6 Localización de raíces
9.7 Número de raíces
9.8 Límites de las raíces reales
9.9 Raíces racionales de una ecuación polinómica
9.10 La ecuación reducida
9.11 Proceso de obtención de todas las raíces racionales
9.12 Regla de Descartes de los signos
9.13 Raíces imaginarias e irracionales

10. FUNCIONES EXPONENCIALES Y LOGARITMICAS
10.1 Funciones exponenciales
10.2 La función exponencial natural
10.3 Funciones logarítmicas
10.4 Gráficas de las funciones exponenciales y logarítmicas
10.5 Logaritmos comunes y naturales
10.6 Ecuaciones exponenciales y logarítmicas
10.7 Definición de funciones hiperbólicas y sus inversas


ESTRUCTURA CONCEPTUAL DE LA MATERIA:

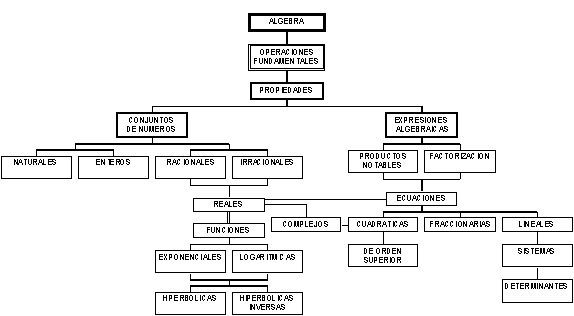
BIBLIOGRAFIA BASICA:

• W. Fleming & D. Vanverg, ALGEBRA LINEAL Y TRIGONOMETRIA CON GEOMETRIA ANALITICA, Prentice Hall Hispanoamericana, México.
• G. Fuller, W. L. Wilson y H. C. Miller, ALGEBRA UNIVERSITARIA, CECSA, México.

BIBLIOGRAFIA COMPLEMENTARIA:

• Reess & Sparks, ALGEBRA, Mc Graw-Hill, NY
• E.P. Vance, ALGEBRA Y TRIGONOMETRIA, Fondo Educativo Interamericano. USA.

MODALIDADES DE EVALUACION: Tareas.Actividades complementarias.Exámenes parciales.
MATERIALES DE APOYO ACADEMICO: Pizarrón y gis. Acetatos y transparencias. Guía de estudios. Problemario. Notas de clase. Proyectos de investigación
MODALIDADES DEL PROCESO ENSEÑANZA APRENDIZAJE: La idea es que el curso no se convierta en una repetición de lo que se estudia en el bachillerato y tampoco se convierta en sesiones de resolución numérica de ejercicios sino que en base a la experiencia de los estudiantes se introduzcan los conceptos más importantes, poniendo énfasis en aquellos tópicos que tradicionalmente no son estudiados en el bachillerato. Se pretende que este curso sea un enlace entre la matemática del bachillerato y la matemática que se abordará en los cursos posteriores. En relación a la vinculación con casos prácticos o aplicaciones no se pretende que se lleve a cabo en este curso pues ellas serán abordadas en otras partes de cada plan de estudios y aquí lo que se busca es la comprensión y adquisición de los conocimientos matemáticos básicos para su posterior uso en las diferentes materias que integren cada plan de estudios. Se utilizaran los siguientes medios en el proceso de enseñanza: Exposición oral
Solución de problemas
Investigación bibliográfica
Realización de trabajos escritos por parte del alumno
Tareas
Exámenes parciales por escrito

CONOCIMIENTOS, APTITUDES, VALORES QUE EL ALUMNO DEBE ADQUIRIR CON BASE AL DESARROLLO DE LA UNIDAD: El estudiante tendrá el dominio conceptual integro de los diferentes tópicos comprendidos en el estudio del álgebra lo que generará en el una facilidad para enfrentar los problemas futuros que comprenden modelos relacionados al álgebra
CAMPO DE APLICACION PROFESIONAL: El alumno será capaz de identificar claramente los modelos matemáticos básicos involucrados en los problemas que se le presenten durante el ejercicio de su profesión.