NOMBRE DE LA MATERIA: MT352 ANÁLISIS CONVEXO
DEPARTAMENTO DE ADSCRIPCION: DEPARTAMENTO DE MATEMÁTICAS
CARGA HORARIA: TEORÍA: 100 PRÁCTICA: 0
CREDITOS: 13
TIPO: CURSO
AREA DE FORMACION: OPTATIVA
PREREQUISITOS: MT210 ANALISIS REAL I

OBJETIVO GENERAL.
 Conocer formalmente el análisis convexo en espacios de dimensión finita.

 OBJETIVOS ESPECIFICOS:
 El alumno:
  1. Comprenderá las principales características de las variedades en Rn y variedades afin en Rn, manejando los conceptos de combinación lineal, independencia, hiperplano, ortogonalidad, subespacios y semiespacios en Rn.

  2. Analizará las propiedades topológicas elementales de conjuntos, polígonos y politopos convexos.

  3. Distinguirá los principales conceptos de dualidad y dualidad polar.

CONTENIDO TEMATICO

1. Variedades Afines en IRn

1.1 Combinaciones lineales que preservan conjuntos paralelos a un subespacio: combinaciones afines y variedades afines.
1.2 Cápsula afín de un subconjunto de IRn.
1.3 Independencia afín, base afín y teorema de representación de Carathéodory.
1.4 Variedades afines de dimensión máxima: hiperplanos.
1.5 Normal de un hiperplano como complemento ortogonal.
1.6 Proyecciones ortogonales; proyección del origen en un hiperplano.
1.7 Altura de un hiperplano como distancia al origen.
1.8 Semiespacios y desigualdades lineales.

 2. Conjuntos Convexos en IRn: Conceptos Básicos
2.1 Segmentos y combinaciones convexas.
2.2 Conjuntos convexos.
2.3 Cápsula convexa de un subconjunto de IRn.
2.4 Teorema de Carathéodory para cápsulas convexas.
2.5 Conos y conos convexos.
2.6 Combinaciones positivas.
2.7 El vértice de un cono: independencia positiva.
2.8 La cápsula convexa de un conjunto afinmente independiente: símplices
y símplices standar en IRn.
2.9 Baricentro y coordenadas baricéntricas.
2.10 El simplex standar como conjunto de distribuciones finitas de probabilidad.
2.11 La dimensión de un conjunto convexo.
2.12 Inclusión de un simplex en todo convexo.
2.13 Operaciones algebraicas con convexos; convexidad de la suma.

 3. Propiedades Topológicas Elementales
3.1 Cápsula convexa de un conjunto abierto.
3.2 Segmentos de puntos interiores a puntos de frontera.
3.3 Intersección de un segmento y la frontera de un convexo.
3.4 No vacuidad del interior relativo y no convexidad de la frontera de un
conjunto convexo.
3.5 Cápsula convexa de un conjunto cerrado; el caso particular de un
compacto.
3.6 Homeomorfismo de compactos convexos de la misma dimensión.
4. Separación, Soporte y Extremos
 4.1 Hiperplanos cota, separadores y soporte de un convexo.
4.2 Separación estricta.
4.3 Existencia de hiperplanos cota.
4.4 Condiciones de separación.
4.5 Teorema del hiperplano soporte.
4.6 Subconjuntos extremos y expuestos; puntos extremos y puntos expuestos.
4.7 Máximos y mínimos de funciones lineales en conjuntos convexos.
5. Funciones Cóncavas y Convexas de IRn a IR.

5.1 Funciones cuasicóncavas y conjuntos de nivel.
5.2 Funciones cóncavas y sus hipográficas.
5.3 Las topologías de orden superior e inferior de los reales, conjuntos de nivel
y funciones semicontinuas: semicontinuidad superior de una función
cuasicóncava.
5.4 Funciones cuasicóncavas homogéneas.
5.5 Funciones cuasiconvexas, convexas y sus epigráficas.
5.6 Soportes de hipográficas y epigráficas.
5.7 Continuidad de funciones cóncavas.
5.8 Derivabilidad de funciones cóncavas y el teorema del hiperplano soporte.
5.9 Funciones seudocóncavas derivables y puntos críticos.
5.10 Máximos locales de funciones cóncavas.
5.11 Funciones cóncavas de clase C2.

 6. Dualidad Polar
6.1 Conjuntos polares de subconjuntos arbitrarios de IRn.
6.2 Propiedades de la relación de polaridad: inversión de operaciones algebraicas
y de conjuntos; reflexividad para convexos cerrados.
6.3 Conos polares.
6.4 Conos sólidos y el vértice del polar.
6.5 Polaridad y ortogonalidad: teorema de la suma directa.
6.6 La función soporte de un conjunto convexo.
6.7 El calibre de un vector respecto a un conjunto convexo.
6.8 Dualidad entre calibres y soportes.
6.9 La norma de Minkowski.
6.10 Teorema de dualidad de Shephard.

  
 
7. Poliedros Convexos
7.1 Politopos como cápsulas convexas de conjuntos finitos.
7.2 Puntos extremos, vértices y puntos expuestos de un poliedro compacto.
7.3 Máximos y mínimos de funciones lineales en poliedros convexos.
7.4 Poliedros descritos por sistemas de desigualdades; identificación de sus
vértices.
7.5 Conos poliédricos y el teorema de Weyl.
7.6 Polares de conos poliédricos y el lema de Farkas.
7.7 El teorema de dualidad de la programación lineal.

 8. Acotamiento, Recesión y aproximación
8.1 Direcciones de recesión de un conjunto convexo.
8.2 El cono asintótico y el cono de recesión.
8.3 Conjuntos acotados y su cono de recesión.
8.4 Conjuntos acotados en una dirección y sus direcciones de recesión.
8.5 Bases positivas y teorema de la base positiva.
8.6 Teorema de Krein-Milman y lema de Shapley-Folkman.


 
 
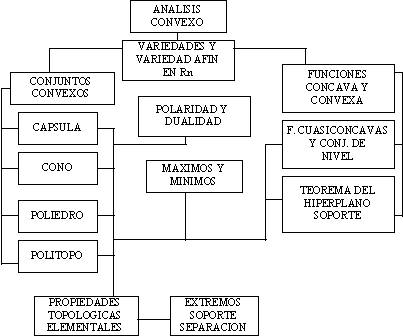
ESTRUCTURA CONCEPTUAL DE LA MATERIA




 
BIBLIOGRAFIA BASICA:

-Uribe, P. Bases Matemáticas para el Análisis Económico. (En proceso de edición).

 BIBLIOGRAFIA COMPLEMENTARIA:

 -Avriel, M., W. E. Diewert, S. Schaible E. I. Zang (1988) Generalized Concavity. N. York y Londres, Plenum Press.

-Lay, S. (1982) Convex Sets and Apllications N. York, Academic Press.

-Nikaido, H. (1968) Convex Structures and Economic Theory. N. York, Academic Press.

-Rockafellar, R.T. (1970) Convex Analysis. Princeton, N.J., Princeton University Press.

-Stoer, J. y C. Witzgall (1970) Convexity and Optimization in Finite Dimensions. Berlin y Heidelberg, Springer Verlag.

 
 
 MODALIDAD DEL PROCESO ENSEÑANZA APRENDIZAJE:

Se pretende en este curso desarrollar habilidades deductivas formales en el alumno, así como proporcionarle un marco teórico ideal para adquirir el nivel de abstracción requerido. Además, se busca presentarle los fundamentos formales de la optimización matemática previa a un curso de economía matemática y teoría de juegos.

 MODALIDADES DE EVALUACION:
 Tareas
Actividades complementarias
Exámenes parciales

 MATERIALES DE APOYO ACADEMICO:
 Pizarrón y gis
Acetatos y transparencias
Guia de estudios
Problemario