NOMBRE DE LA MATERIA: MT240 ECUACIONES DIFERENCIALES ORDINARIAS II
DEPARTAMENTO DE ADSCRIPCION: DEPARTAMENTO DE MATEMATICAS
CARGA HORARIA SEMESTRAL: TEORIA: 100 PRACTICA: 0
CREDITOS: 13
TIPO: CURSO
AREA DE FORMACION: BASICA PARTICULAR OBLIGATORIA
PREREQUISITOS: MT140 ECUACIONES DIFERENCIALES ORDINARIAS I

OBJETIVO GENERAL:
El alumno comprenderá y analizará algunos tipos de ecuaciones diferenciales ordinarias y sistemas de ecuaciones diferenciales ordinarias así como los métodos para su solución y las soluciones de dichas ecuaciones y sistemas.

OBJETIVOS ESPECIFICOS:
  1. El alumno será capaz de seleccionar correctamente el método de solución de una ecuación diferencial ordinaria ó sistemas de ecuaciones diferenciales ordinarias dado y la resolverá.
  2. El alumno analizará las soluciones del tipo de ecuaciones diferenciales ordinarias aprendidas y demostrará el teorema de existencia y unicidad de soluciones.

CONTENIDO:

1. PROBLEMAS DE STURM-LIOUVILLE (12 HORAS).
OBJETIVO PARTICULAR: El alumno reconocerá y resolverá un sistema de Sturm-Liouville y analizará las características de estos y sus soluciones.
1.1. Definiciones (3 horas)
1.2. Teorema de ortogonalidad (4 horas)
1.3. Sistema de regular y periódico de Sturm-Liouville (1 hora)
1.4. Series de Sturm-Liouville (2 horas)
2. SOLUCION EN SERIE DE POTENCIAS DE LAS ECUACIONES DIFERENCIALES (27 HORAS).
OBJETIVO PARTICULAR: El profesor expondrá a los alumnos el método de solución en serie de potencias para resolver una ecuación diferencial ordinaria lineal.
2.1. Series de potencias (3 horas)
2.2. Método de los coeficientes indeterminados (3 horas)
2.3. Solución en serie de potencias alrededor de un punto ordinario (3 horas)
2.3.1. Ecuación de Legendre (1 hora)
2.3.1.1. Polinomios de Legendre (2 horas)2.4. Solución en serie de potencias alrededor de un punto singular regular (1 hora)
2.4.1. Método de Frobenius (6 horas)
2.4.1.1. Ecuación de Bessel (6 horas)
3. SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS (27 HORAS)
OBJETIVO PARTICULAR: El alumno conocerá y analizará la teoría para encontrar las soluciones de un sistema de ecuaciones diferenciales ordinarias lineales de 1er. orden en forma normal.
3.1. Definiciones (3 horas)
3.2. Sistema lineal homogéneo de 1er. orden con coeficientes constantes en forma normal (3 horas)
3.2.1. Sistema acoplado (2 horas)
3.2.2. Sistema desacoplado (1 hora)
3.2.2.1. Diagonalización y método de solución (7 horas)3.2.3. La matriz fundamental de soluciones eAt (2 horas)3.3. Sistema lineal no homogéneo de 1er. orden en forma normal (2 horas)
3.3.1. Método de coeficientes indeterminados (1 hora)
3.3.2. Método de variación de parámetros (4 horas)
4. TEOREMA DE EXISTENCIA Y UNICIDAD (20 HORAS)
OBJETIVO PARTICULAR: El profesor mostrará un conjunto de teoremas a partir de los cuales el alumno inferirá la demostración del teorema de existencia y unicidad de soluciones de ecuaciones diferenciales ordinarias.
4.1. Introducción (1 hora)
4.2. Condición de Lipschitz (6 horas)
4.3. Teorema de unicidad (2 horas)
4.4. Continuidad (3 horas)
4.5. Ecuación Integral equivalente (1 hora)
4.6. Aproximaciones sucesivas (3 horas)
4.7. Teorema de existencia local (1.5 horas)
4.8. Continuación de la solución (2.5 horas)
5. ESTABILIDAD (14 HORAS)
OBJETIVO PARTICULAR: El alumno distinguirá y analizará los puntos críticos de un sistema de ecuaciones diferenciales ordinarias y entonces determinará su estabilidad.
5.1. Introducción (3 horas)
5.2. Puntos críticos y su estabilidad (6 horas)
5.3. Linealización (3 horas)
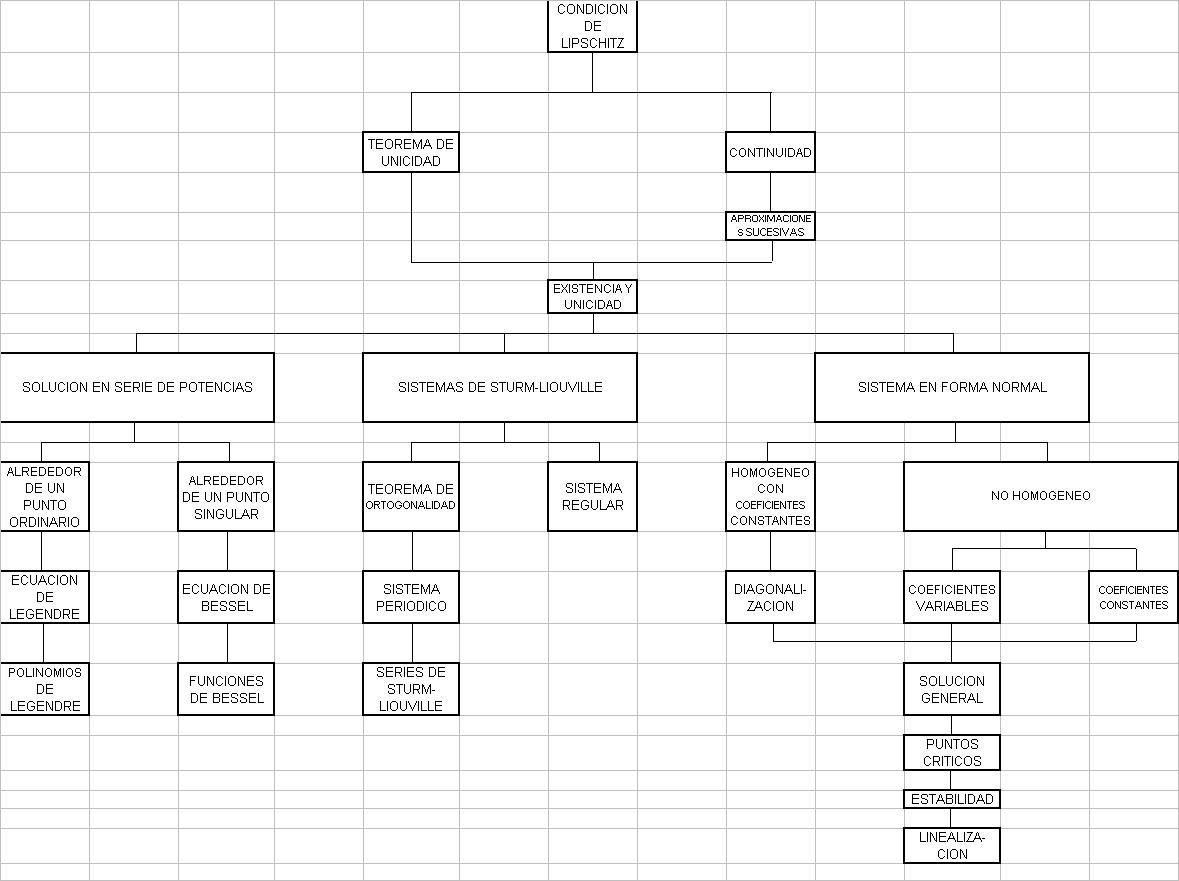
ESTRUCTURA CONCEPTUAL DE LA MATERIA:



BIBLIOGRAFIA BASICA
 · S. L. Ross, ECUACIONES DIFERENCIALES, John Wiley & Sons.
· Erwin Kreyszig, ADVANCED ENGINEERING MATHEMATICS, John Wiley & Sons.
· Lawrence Perko, DIFFERENTIAL EQUATIONS AND DYNAMICAL SYSTEMS, Springer.

BIBLIOGRAFIA COMPLEMENTARIA
 · Garrett Birkhoff y Gian-Carlo Rota, ORDINARY DIFFERENTIAL EQUATIONS, John Wiley & Sons.
· S. L. Ross, INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES, Interamericana

MODALIDAD DE EVALUACIÓN:
Tareas. Exámenes parciales.

MATERIALES DE APOYO ACADEMICO:
Pintarrón y plumón, prácticas en laboratorio de computo.

MODALIDADES DEL PROCESO ENSEÑANZA APRENDIZAJE:
Se pretende hacer una clase participativa, que el alumno utilice lo aprendido para razonar e inferir nuevos conocimientos.
Se utilizaran los siguientes medios en el proceso de enseñanza:


CAMPO DE APLICACIÓN PROFESIONAL:
Este curso proporciona al alumno una herramienta básica para trabajar el área de las matemáticas aplicadas.