NOMBRE DE LA MATERIA: MT150 ELEMENTOS DE PROBABILIDAD Y ESTADISTICA
DEPARTAMENTO DE ADSCRIPCION: DEPARTAMENTO DE MATEMATICAS
CARGA HORARIA SEMESTRAL: TEORIA: 60 PRACTICA: 0
CREDITOS: 8 TIPO: CURSO
AREA DE FORMACION: BASICA COMUN
PREREQUISITOS: NINGUNO

OBJETIVO GENERAL:
Identificar la naturaleza de la probabilidad y la estadística, sus objetivos y de como desempeña un papel importante en las ciencias, la industria y en la vida diaria.

OBJETIVOS ESPECIFICOS:
El alumno desarrollará las técnicas para la presentación y descripción de datos.El alumno adquirirá los conocimientos teóricos básicos para el análisis de datos. El alumno podrá inferir sobre una población a partir de datos muestrales.

CONTENIDO TEMATICO:
1. INTRODUCCION (1 hr.)

2. DESCRIPCION DE UN CONJUNTO DE DATOS (8 hrs.)
2.1 Descripción numérica de un conjunto de datos
2.1.1 Medidas de tendencia central (2 hrs.)
2.1.2 Medidas de Dispersión (1 hr.)
2.1.3 Regla Empírica (1 hr.)2.2 Descripción gráfica de un conjunto de datos
2.2.1 Histograma y tabla de frecuencias (1 hr.)
2.2.2 Diagrama de caja (0.5 hr.)2.3 Descripción de datos categóricos
2.3.1 Diagrama de barras y gráfica circular (0.5 hr.)
2.3.2 Diagrama de Pareto (1 hr.) 2.4 Errores típicos (1 hr.)

3. RELACION ENTRE DOS CONJUNTOS DE DATOS (3 hrs.)
3.1 Diagrama de dispersión (1 hr.)
3.2 Coeficiente de correlación (1 hr.)
3.3 Recta de regresión (1 hr.)

4. CONCEPTOS BASICOS DE PROBABILIDAD (11 hrs.)
4.1 Experimento, espacio muestral y evento (1 hr.)
4.2 Reglas de probabilidad
4.2.1 Regla de la adición (1.5 hrs.)
4.2.2 Regla de la multiplicación (1 hr.)
4.3 Independencia y probabilidad condicional (1 hr.)
4.4 Variables aleatorias discretas (0.5 hr.)
4.5 Variables aleatorias continuas (0.5 hr.)
4.6 Función de probabilidad (0.5 hr.)
4.7 Función de densidad de probabilidades (1 hr.)
4.8 Función de distribución acumulada (1 hr.)
4.9 Esperanza y varianza (1 hr.)
4.10 Teorema de Chebyshev (2 hrs.)

5. MODELOS PROBABILISTICOS (7 hrs.)
5.1 Experimento de Bernoulli (0.5 hr.)
5.2 Distribución de Bernoulli (0.5 hr.)
5.3 Distribución Binomial (1 hr.)
5.4 Distribución Hipergeométrica (1 hr.)
5.5 Distribución de Poisson (1 hr.)
5.6 Distribución normal (2 hrs.)
5.7 Distribución uniforme (1 hr.)

6. DISTRIBUCIONES DERIVADAS DEL MUESTREO, ESTIMACIÓN Y PRUEBA DE HIPÓTESIS (15 hrs.)
6.1 Población y muestra (0.5 hr.)
6.2 Estadísticos y sus distribuciones (0.5 hr.)
6.3 Distribución muestral normal (1 hr.)
6.4 Estimadores y sus propiedades (1 hr.)
6.5 Estimación puntual y por intervalo de una media con n > 30 (1 hr.)
6.6 Estimación puntual y por intervalo de una proporción (1 hr.)
6.7 Hipótesis estadística (1 hr.)
6.8 Errores tipo I y tipo II (0.5 hr.)
6.9 Prueba de hipótesis para diferencia de medias n > 30 (1 hr.)
6.10 Prueba de hipótesis para diferencia de proporciones (1 hrs.)
6.11 Distribución muestral t de Student (1 hr.)
6.12 Estimación puntual y por intervalo de una media con n <= 30 (1 hr.) 6.13 Prueba de hipótesis para diferencia de media n <= 30 (1 hrs.) 6.14 Distribución ji-cuadrada (0.5 hr.)
6.15 Estimación de la varianza (0.5 hr.)
6.16 Comparación de una varianza poblacional (1 hrs.)
6.17 Distribución muestral F de Snedecor (0.5 hr.)
6.18 Comparación de dos varianzas poblacionales (1 hrs.)

ESTRUCTURA CONCEPTUAL DE LA MATERIA:


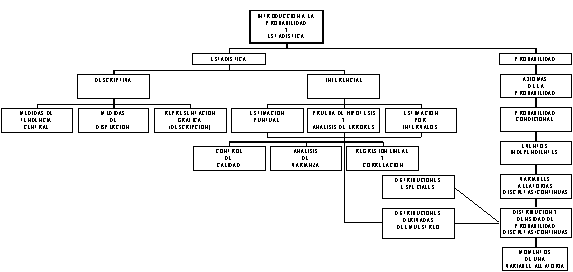
BIBLIOGRAFIA BASICA:
BIBLIOGRAFIA COMPLEMENTARIA:
MODALIDADES DE EVALUACION: Tareas.Actividades complementarias.Exámenes parciales.
MATERIALES DE APOYO ACADEMICO: Pizarrón y gis. Acetatos y transparencias. Guía de estudios. Problemario. Notas de clase. Proyectos de investigación
MODALIDADES DEL PROCESO ENSEÑANZA APRENDIZAJE:
La idea es que el curso no se convierta en una repetición de lo que se estudia en el bachillerato y tampoco se convierta en sesiones de resolución numérica de ejercicios sino que en base a la experiencia de los estudiantes se introduzcan los conceptos más importantes, poniendo énfasis en aquellos tópicos que tradicionalmente no son estudiados en el bachillerato. Se pretende que este curso sea un enlace entre la matemática del bachillerato y la matemática que se abordará en los cursos posteriores. En relación a la vinculación con casos prácticos o aplicaciones no se pretende que se lleve a cabo en este curso pues ellas serán abordadas en otras partes de cada plan de estudios y aquí lo que se busca es la comprensión y adquisición de los conocimientos matemáticos básicos para su posterior uso en las diferentes materias que integren cada plan de estudios. Se utilizaran los siguientes medios en el proceso de enseñanza: Exposición oral
Solución de problemas
Investigación bibliográfica
Realización de trabajos escritos por parte del alumno
Tareas
Exámenes parciales por escrito

CONOCIMIENTOS, APTITUDES, VALORES QUE EL ALUMNO DEBE ADQUIRIR CON BASE AL DESARROLLO DE LA UNIDAD:
El estudiante tendrá el dominio conceptual integro de los diferentes tópicos comprendidos en el estudio de la probabilidad y la estadística.Tendrá la capacidad de manejar conjuntos de datos para analizarlos o inferir sobre ellos en problemas que comprendan diferentes áreas del conocimiento donde se recopilen datos para su estudio.

CAMPO DE APLICACION PROFESIONAL:
El alumno será capaz de identificar claramente los modelos matemáticos básicos involucrados en los problemas que se le presenten durante el ejercicio de su profesión